Zero Knowledge Proof Học bằng cách viết mã: Bắt đầu với libsnark

特邀专栏作者

2020-01-03 10:19

Bài viết này có khoảng 17557 từ, đọc toàn bộ bài viết mất khoảng 26 phút

Tôi hy vọng rằng thông qua loạt bài viết này, tất cả các nhà phát triển có thể bắt đầu với libsnark trong một khoảng thời gian ngắn và hiểu từng bước các khái niệm cơ bản về libsnark.

Tác giả bài viết: p0n1@安比实验

libsnark hiện là khuôn khổ quan trọng nhất để triển khai các mạch zk-SNARK và được sử dụng rộng rãi trong nhiều giao dịch cá nhân hoặc các dự án liên quan đến điện toán bảo mật, trong đó Zcash là nổi tiếng nhất. Zcash đã sử dụng libsnark để triển khai các mạch cho đến khi phiên bản Sapling được nâng cấp (sau này nó được thay thế bằng bellman). Không ngoa khi nói rằng libsnark hỗ trợ và thúc đẩy ứng dụng quy mô lớn đầu tiên của công nghệ zk-SNARKs, lấp đầy khoảng cách giữa lý thuyết mới nhất và triển khai kỹ thuật của công nghệ bằng chứng không kiến thức.

Tôi hy vọng rằng thông qua loạt bài viết này, tất cả các nhà phát triển có thể bắt đầu với libsnark trong một khoảng thời gian ngắn, từng bước hiểu các khái niệm cơ bản về libsnark, tìm hiểu cách phát triển các mạch zk-SNARK, hoàn thành việc tạo và xác minh bằng chứng, và cuối cùng là chuyển đổi Zero-knowledge Proof áp dụng vào kinh doanh thực tế.

1. Giới thiệu về nền tảng của zk-SNARK và libsnark

Bằng chứng không kiến thức có thể là công nghệ đen mã hóa giàu trí tưởng tượng và hứa hẹn nhất hiện nay. Còn zk-SNARKs là tên viết tắt của một loại zero-knowledge proof scheme, tên đầy đủ là Zero-Knowledge Succinct Non-interactive Arguments of Knowledge. Tên này chứa gần như tất cả các tính năng kỹ thuật của nó, nghĩa là tính đúng đắn của một đề xuất có thể được chứng minh mà không tiết lộ bất kỳ thông tin nào khác và bằng chứng được tạo ra cuối cùng là ngắn gọn (Succinct), có nghĩa là bằng chứng được tạo ra cuối cùng đủ nhỏ và có không có gì để làm với số lượng tính toán, nó là một hằng số. Nói một cách đơn giản, về mặt lý thuyết, bạn có thể chứng minh điều gì đó với những người khác mà không để lộ bất kỳ quyền riêng tư nào và bằng chứng được tạo có kích thước nhỏ và chi phí xác minh rất thấp, bất kể số lượng tính toán cần thiết để chứng minh nội dung. Âm thanh đơn giản là quá tốt để trở thành sự thật!

zk-SNARK có thể được áp dụng cho nhiều tình huống, chẳng hạn như bảo vệ quyền riêng tư, mở rộng chuỗi khối, điện toán có thể kiểm chứng, v.v. Bài viết này không giới thiệu chi tiết lý thuyết về zk-SNARKS và bằng chứng zero-knowledge, sinh viên nào chưa hiểu hoặc muốn tìm hiểu thêm có thể đọc các bài viết hoặc tài liệu khác.

Chẳng hạn như ba bài đăng trên blog nổi tiếng của Vitalik về zk-SNARK.

https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649
https://medium.com/@VitalikButerin/exploring-elliptic-curve-pairings-c73c1864e627
https://medium.com/@VitalikButerin/zk-snarks-under-the-hood-b33151a013f6

Hoặc đọc những gì Xiang Cheng @HUST đã viết"Zk-SNARK về bằng chứng không kiến thức bằng thuật ngữ đơn giản", và Dongze đã viết"Nói về bằng chứng không kiến thức II: bằng chứng không tương tác ngắn (SNARK)"。

Tất nhiên, chào mừng bạn chú ý đến Ambi LabVàVàLoạt bài "Học zk-SNARK từ đầu"và từ Ambi Labs đã duy trì"Tóm tắt tài nguyên học tập chứng minh tri thức bằng không"Tìm thêm thông tin trong.

Nhân vật chính của bài viết này, libsnark, là một thư viện mã C++ để phát triển các ứng dụng zk-SNARK, được phát triển và duy trì bởi SCIPR Lab. Cơ sở lý thuyết đằng sau việc triển khai kỹ thuật libsnark là một loạt các bài báo quan trọng theo hướng bằng chứng không kiến thức, đặc biệt là zk-SNARK, trong những năm gần đây (đặc biệt là từ năm 2013). Một số trong những cái nổi tiếng nhất như sau:

[GGPR13] Quadratic span programs and succinct NIZKs without PCPs , Rosario Gennaro, Craig Gentry, Bryan Parno, Mariana Raykova, EUROCRYPT 2013
[PGHR13] Pinocchio: Nearly Practical Verifiable Computation , Bryan Parno, Craig Gentry, Jon Howell, Mariana Raykova, IEEE Symposium on Security and Privacy (Oakland) 2013
[BCGTV13] SNARKs for C: Verifying Program Executions Succinctly and in Zero Knowledge , Eli Ben-Sasson, Alessandro Chiesa, Daniel Genkin, Eran Tromer, Madars Virza, CRYPTO 2013
[BCIOP13] Succinct non-interactive arguments via linear interactive Proofs , Nir Bitansky, Alessandro Chiesa, Yuval Ishai, Rafail Ostrovsky, Omer Paneth, Theory of Cryptography Conference 2013
[BCTV14a] Succinct non-interactive zero knowledge for a von Neumann architecture , Eli Ben-Sasson, Alessandro Chiesa, Eran Tromer, Madars Virza, USENIX Security 2014
[BCTV14b] Scalable succinct non-interactive arguments via cycles of elliptic curves , Eli Ben-Sasson, Alessandro Chiesa, Eran Tromer, Madars Virza, CRYPTO 2014
[Groth16] On the Size of Pairing-based Non-interactive Arguments , Jens Groth, EUROCRYPT 2016

Các nhà phát triển của libsnark cũng là những học giả hoặc chuyên gia nghiên cứu hàng đầu trong lĩnh vực này, chẳng hạn như Eran Tromer, đồng tác giả của nhiều bài báo nói trên.

Nền tảng lý thuyết vững chắc và khả năng kỹ thuật cho phép các tác giả của libsnark đơn giản hóa sự phức tạp, hiện thực hóa các lý thuyết nâng cao và công thức phức tạp được trình bày trong hình bên dưới từng cái một và trừu tượng hóa giao diện ngắn gọn với trình độ kỹ thuật cao để thuận tiện cho các nhà phát triển. Khen ngợi những người tiên phong này, những người đã mở rộng nghiên cứu lý thuyết đặc biệt cho các ứng dụng quy mô lớn hơn.

Hình dưới đây là tổng quan về mô-đun của libsnark, được lấy từ Madars Virza, tác giả đầu tiên của đóng góp mã libsnark, tại MITluận án tiến sĩ。

)

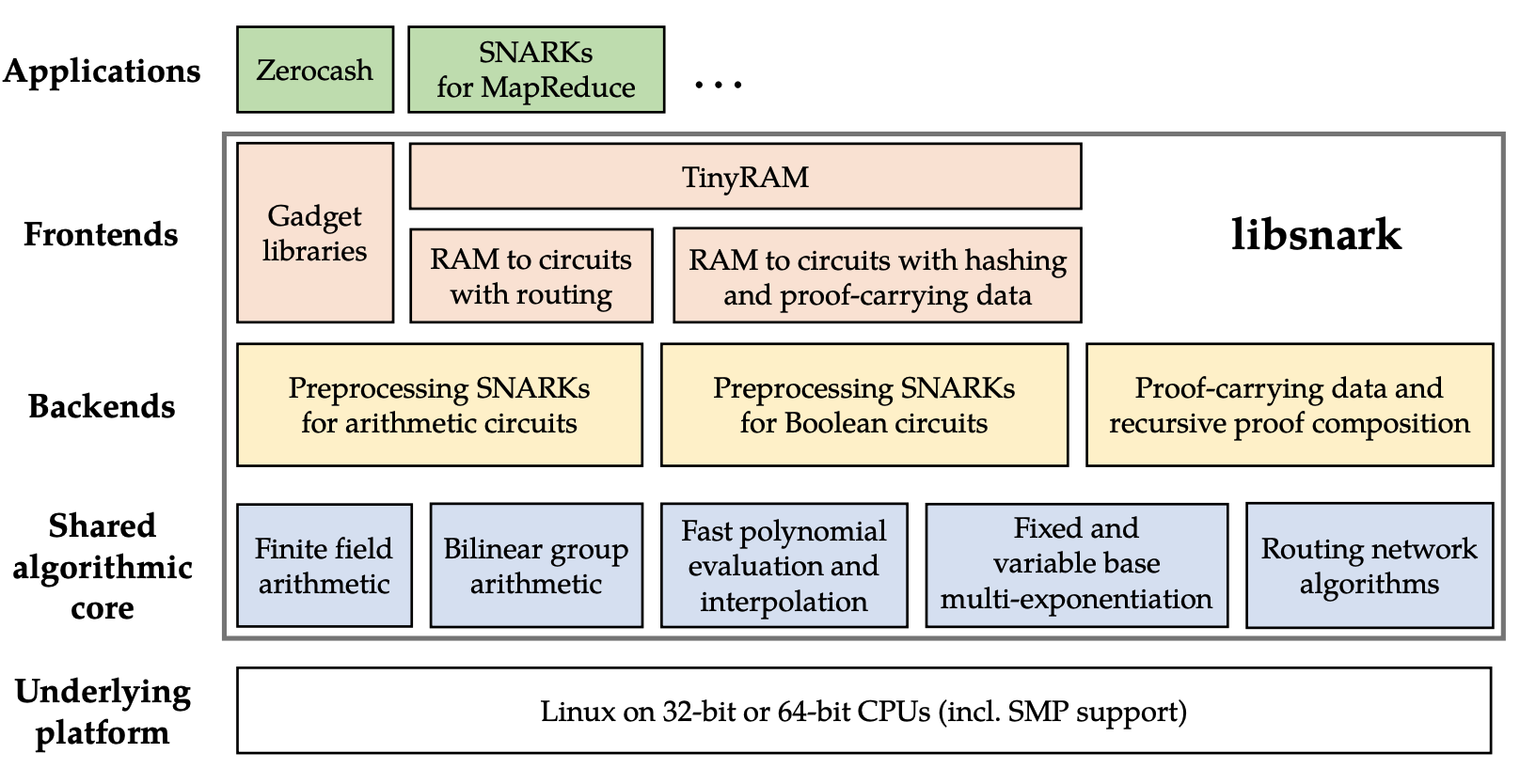
Khung libsnark cung cấp việc triển khai nhiều hệ thống bằng chứng chung, trong đó BCTV14a và Groth16 được sử dụng nhiều hơn.

TRONG:

zk_proof_systems/ppzksnark/r1cs_ppzksnark tương ứng với BCTV14a
zk_proof_systems/ppzksnark/r1cs_gg_ppzksnark tương ứng với Groth16

Nếu bạn muốn nghiên cứu chi tiết việc triển khai của hai giao thức này, bạn có thể bắt đầu trực tiếp từ hai thư mục này. ppzksnark đề cập đến tiền xử lý zkSNARK. PP/tiền xử lý ở đây thực chất đề cập đến thiết lập đáng tin cậy mà chúng ta thường nói, tức là trước khi bằng chứng được tạo và xác minh, cần phải tạo các tham số công khai có liên quan (khóa chứng minh và khóa xác minh) thông qua thuật toán tạo. Chúng tôi cũng gọi tham số được tạo trước này là "Chuỗi tham chiếu chung" (Chuỗi tham chiếu chung) hoặc đơn giản làCRS。

2. Nguyên tắc và các bước cơ bản

Việc sử dụng thư viện libsnark để phát triển các ứng dụng zk-SNARK có thể được tóm tắt ngắn gọn theo bốn bước sau về nguyên tắc:

Biểu thị mệnh đề cần chứng minh là R1CS (Hệ thống ràng buộc hạng một)
Tạo các tham số công khai cho đề xuất này bằng thuật toán tổng quát (G)
Tạo bằng chứng về sự thỏa mãn của R1CS bằng thuật toán chứng minh (P)
Sử dụng thuật toán xác minh (V) để xác minh bằng chứng

bài viết nàybài viết này。

Có một hàm như vậy C(x, out), được sử dụng để đánh giá xem bí mật x có thỏa mãn phương trình x^3 + x + 5 == out hay không và trả về true nếu nó thỏa mãn.

function C(x, out) {
return ( x^3 + x + 5 == out );
}

Ở bước đầu tiên, chúng ta cần biểu diễn hàm C(x, out) trong libsnark. Nó được bỏ qua ở đây và quy trình chi tiết sẽ được giới thiệu sau.

Bước thứ hai, tương ứng với chức năng Trình tạo (G) sau đây, lambda được tạo ngẫu nhiên, thường được cho là được tạo trong quá trình thiết lập đáng tin cậy"toxic waste". Mọi người thích gọi nó là "chất thải độc hại" vì nó phải được xử lý đúng cách (ví dụ: nó phải được tiêu hủy và không ai có thể biết về nó), nếu không nó sẽ ảnh hưởng đến tính bảo mật của giao thức chứng minh.

lambda <- random()

(pk, vk) = G(C, lambda)

Cuối cùng, khóa chứng minh (pk) và khóa xác minh (vk) được tạo.

Bước thứ ba tương ứng với việc sử dụng chức năng Chứng minh (P) để tạo bằng chứng. Điều tôi muốn chứng minh ở đây là người chứng minh biết một giá trị bí mật x và kết quả tính toán có thể thỏa mãn phương trình. Do đó, chuyển x, out và pk làm đầu vào cho P và cuối cùng tạo ra bằng chứng.

proof = P(pk, out, x)

Bước thứ tư là sử dụng chức năng Xác minh (V) để xác minh bằng chứng, chuyển bằng chứng, ra và vk cho G, sau đó chứng minh rằng có một giá trị bí mật thỏa mãn phương trình mà không tiết lộ bí mật.

V(vk, out, proof) ?= true

Khối lượng công việc chính của nhà phát triển tập trung vào bước đầu tiên, bước này cần viết mã mạch C++ để mô tả các đề xuất bằng tay theo quy tắc giao diện của libsnark và xây dựng các ràng buộc R1CS từ mã. Toàn bộ quá trình cũng tương ứng với Tính toán -> Mạch số học -> R1CS trong hình bên dưới.

3. Xây dựng môi trường phát triển ứng dụng zk-SNARKs

Hãy nhập liên kết thực hành, nhanh chóng bắt đầu với libsnark và xem qua các ví dụ.

Trước tiên, hãy tải xuống thư viện mã mẫu tối thiểu có sẵn của libsnark libsnark_abc tương ứng với bài viết này.

git clone https://github.com/sec-bit/libsnark_abc.git

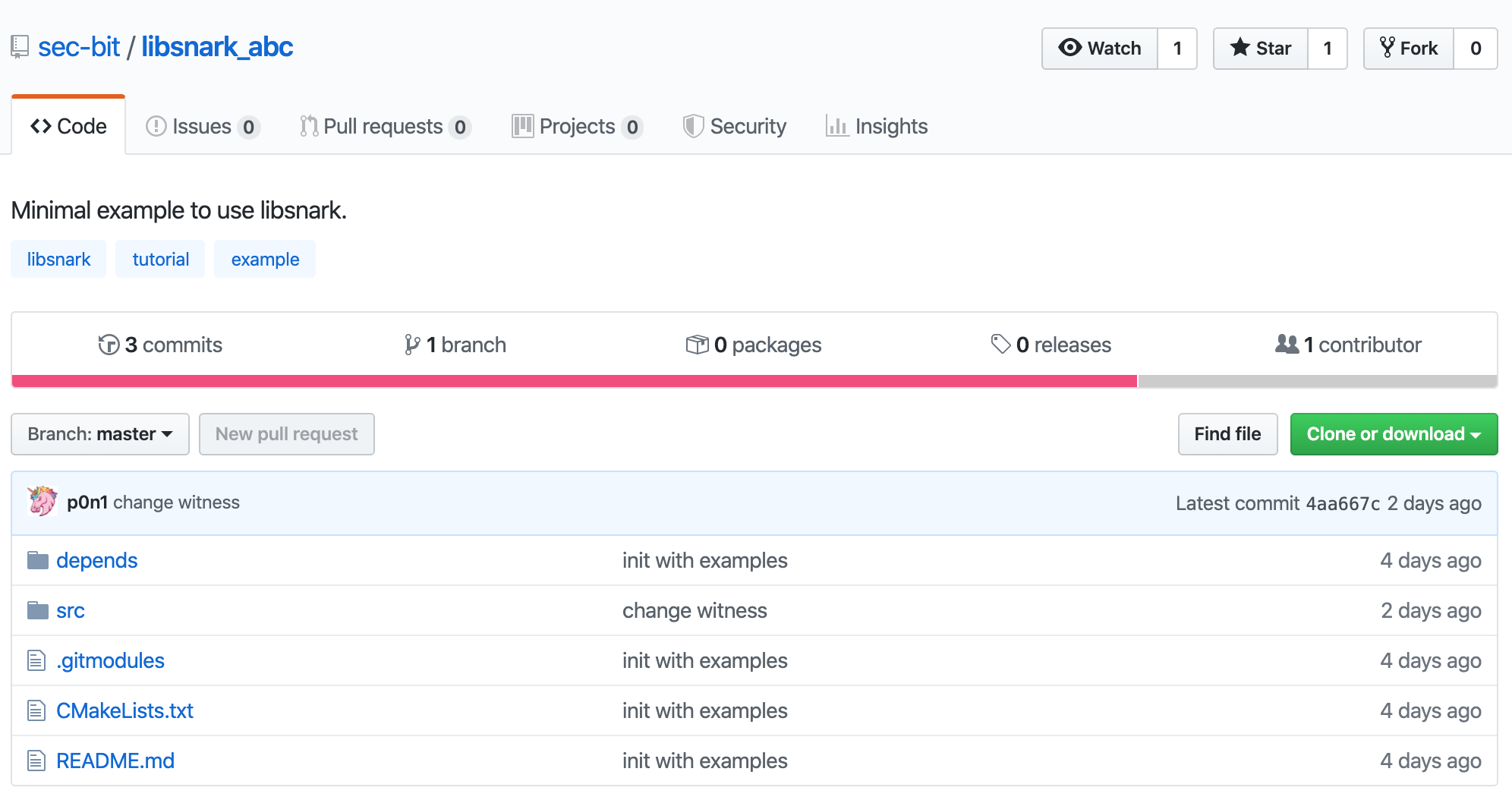
Kéo mã libsnark qua mô hình con git.

cd libsnark_abc
git submodule update --init --recursive

Tham khảo libsnarktài liệu dự ánHoàn thành cài đặt phụ thuộc có liên quan. Lấy Ubuntu 16.04 LTS làm ví dụ, các thành phần sau cần được cài đặt:

sudo apt-get install build-essential cmake git libgmp3-dev libprocps4-dev python-markdown libboost-all-dev libssl-dev

Khởi tạo thư mục bản dựng.

mkdir build && cd build && cmake ..

Bước này có thể gặp sự cố trong hệ thống macOS, tham khảovấn đề nàyđối phó với. hoặc thử sử dụng lệnh sau:

mkdir build && cd build && CPPFLAGS=-I/usr/local/opt/openssl/include LDFLAGS=-L/usr/local/opt/openssl/lib PKG_CONFIG_PATH=/usr/local/opt/openssl/lib/pkgconfig cmake -DWITH_PROCPS=OFF -DWITH_SUPERCOP=OFF ..

Sau khi thành công, nó vẫn được biên dịch trong thư mục bản dựng.

make

Sau khi biên dịch thành công, bạn có thể thấy 3 tệp nhị phân trong thư mục build/src.

main
range
test

Đến đây, bạn đã hoàn thành việc biên soạn dự án mẫu. Hãy thử chạy mã mẫu.

./src/main

Cuối cùng, nhật ký sau xuất hiện, cho biết mọi thứ đều bình thường. Bạn đã sở hữu thành công môi trường phát triển ứng dụng zkSNARK và chạy thành công bản demo zk-SNARKs đầu tiên.

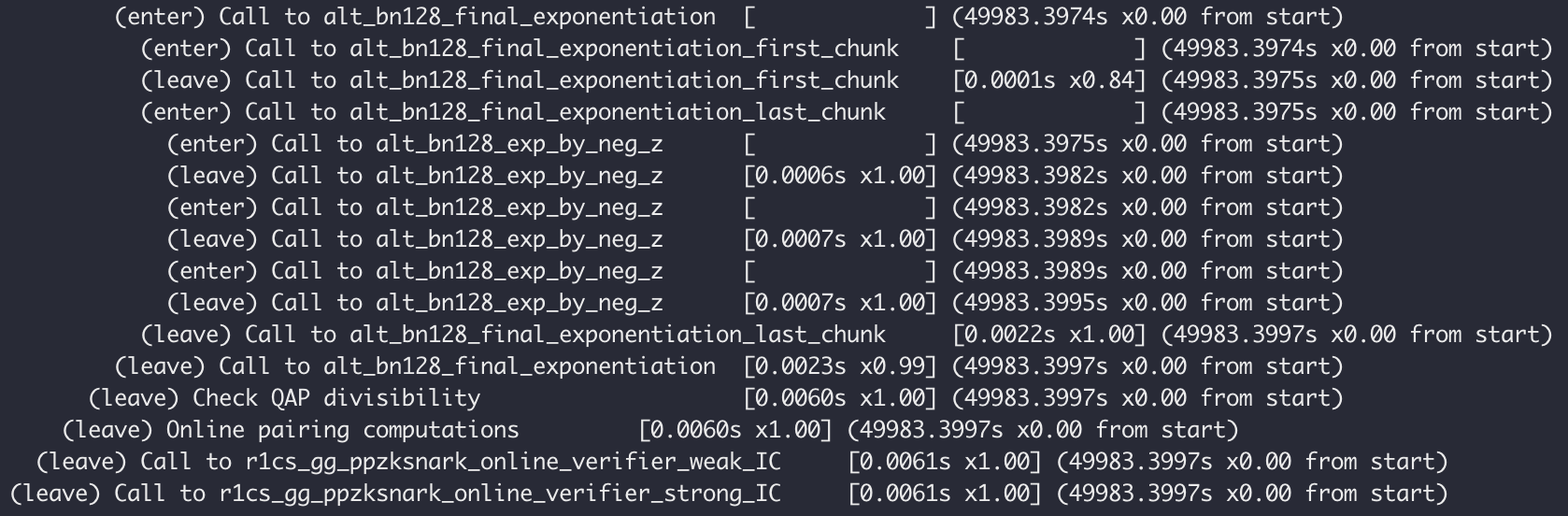
4. Hiểu code mẫu

Chúng ta hãy cùng nhau xem xét kỹ hơn mã. Dự án mẫu gồm 3 mã (xem thêm phụ lục cuối bài).

Trước tiên, hãy xem src/main.cpp. Ví dụ này đến từ Howard Wu'slibsnark_tutorial, ông cũng là một trong những tác giả của libsnark. Cấu trúc project của libsnark_abc trong bài viết này được xây dựng theo libsnark_tutorial của anh ấy, thuộc "phong cách được đề xuất chính thức", các bạn yên tâm mà dùng nhé😆.

Chỉ có hàng chục dòng mã, trong đó run_r1cs_gg_ppzksnark() là phần chính. Thật dễ dàng để thấy rằng mã cơ bản hoạt động thực sự chỉ có 5 dòng sau.

r1cs_gg_ppzksnark_keypair keypair = r1cs_gg_ppzksnark_generator(example.constraint_system);

r1cs_gg_ppzksnark_processed_verification_key pvk = r1cs_gg_ppzksnark_verifier_process_vk(keypair.vk);

r1cs_gg_ppzksnark_proof proof = r1cs_gg_ppzksnark_prover(keypair.pk, example.primary_input, example.auxiliary_input);

const bool ans = r1cs_gg_ppzksnark_verifier_strong_IC(keypair.vk, example.primary_input, proof);

const bool ans2 = r1cs_gg_ppzksnark_online_verifier_strong_IC(pvk, example.primary_input, proof);

Bạn có thể thấy từng bước đang làm gì chỉ từ tên chức năng "siêu dài", nhưng bạn không thể xem chi tiết cách xây dựng mạch. Trên thực tế, ở đây chỉ gọi r1cs_example tích hợp, ẩn các chi tiết triển khai.

Trong trường hợp đó, chúng ta hãy tìm hiểu chi tiết mạch thông qua một ví dụ trực quan hơn. Nghiên cứu src/test.cpp, ví dụ này được phỏng theo Christian Lundkvist'slibsnark-tutorial。

Chỉ có ba tệp tiêu đề được tham chiếu ở đầu mã, cụ thể là:

#include
#include
#include

Như đã đề cập trước đó, r1cs_gg_ppzksnark tương ứng với sơ đồ Groth16. Cái gg được thêm vào đây để phân biệt r1cs_ppzksnark (tức là BCTV14a scheme), có nghĩa là Generic Group Model (mô hình nhóm chung). Bằng chứng bảo mật của Groth16 dựa trên Mô hình nhóm chung, mô hình này đánh đổi các giả định bảo mật mạnh hơn để có hiệu suất tốt hơn và bằng chứng ngắn hơn.

Tệp tiêu đề đầu tiên là giới thiệu loại default_r1cs_gg_ppzksnark_pp và tệp thứ hai là giới thiệu các giao diện khác nhau liên quan đến bằng chứng. pb_variable được sử dụng để xác định các biến liên quan đến mạch.

Tiếp theo, một số khởi tạo được yêu cầu để xác định trường hữu hạn được sử dụng và khởi tạo các tham số đường cong. Điều này tương đương với mọi sự chuẩn bị.

typedef libff::Fr FieldT;
default_r1cs_gg_ppzksnark_pp::init_public_params();

Tiếp theo, cần làm rõ “mệnh đề cần chứng minh” là gì. Ở đây chúng ta cũng có thể sử dụng ví dụ trước để chứng minh rằng bí mật x thỏa mãn phương trình x^3 + x + 5 == out. Đây thực sự là một bài đăng trên blog của Vitalik"Quadratic Arithmetic Programs: from Zero to Hero"Các ví dụ được sử dụng trong . Nếu bạn chưa quen với những thay đổi bên dưới, hãy thử đọc bài đăng trên blog này.

Bằng cách giới thiệu các biến trung gian sym_1, y và sym_2, x^3 + x + 5 = out được làm phẳng thành một số phương trình bậc hai và một số biểu thức chỉ liên quan đến phép nhân hoặc phép cộng đơn giản tương ứng với cổng nhân và phép cộng trong mạch số học. . Bạn có thể dễ dàng vẽ mạch tương ứng trên giấy.

x * x = sym_1
sym_1 * x = y
y + x = sym_2
sym_2 + 5 = out

Thông thường bài viết ở đây sẽ giới thiệu cách sắp xếp các phương trình trên dưới dạng R1CS, và từng bước suy ra vector tương ứng cụ thể. Điều này hữu ích để hiểu cách chuyển đổi Gate thành R1CS, nhưng nó không phải là mục đích cốt lõi của bài viết này. Vì vậy, một trăm từ được bỏ qua ở đây.

Các biến liên quan đến đề xuất được xác định dưới đây. Protoboard được tạo ra đầu tiên là một khái niệm quan trọng trong libsnark. Như tên của nó, nó là một bo mạch nguyên mẫu hoặc bo mạch bánh mì, được sử dụng để nhanh chóng xây dựng một mạch. Trong mạch zk-SNARK, nó được sử dụng để liên kết tất cả các biến, thành phần và hạn chế. Đoạn mã sau định nghĩa tất cả các biến yêu cầu đầu vào bên ngoài và các biến trung gian.

// Create protoboard
protoboard pb;

// Define variables
pb_variable x;
pb_variable sym_1;
pb_variable y;
pb_variable sym_2;
pb_variable out;

Tiếp theo, kết nối từng biến với protoboard, tương đương với việc chèn từng thành phần vào "bảng mạch". Biến kiểu chuỗi thứ hai của hàm phân bổ() chỉ được sử dụng cho nhận xét trong quá trình GỠ LỖI và thuận tiện để xem nhật ký trong quá trình GỠ LỖI.

out.allocate(pb, "out");
x.allocate(pb, "x");
sym_1.allocate(pb, "sym_1");
y.allocate(pb, "y");
sym_2.allocate(pb, "sym_2");
pb.set_input_sizes(1);

Lưu ý rằng kết nối đầu tiên tới pb ở đây là biến out. Chúng tôi biết rằng có các khái niệm đầu vào công khai và nhân chứng riêng trong zk-SNARK, tương ứng với các biến chính và biến phụ trong libsnark. Vậy làm thế nào để tạo ra sự khác biệt trong mã? Chúng ta cần sử dụng set_input_sizes(n) để khai báo số n biến công khai/chính được kết nối với protoboard. Ở đây n = 1, chỉ ra rằng n = 1 biến đầu tiên được kết nối với pb là công khai và phần còn lại là riêng tư.

Cho đến nay, tất cả các biến đã được kết nối thành công với tấm nguyên mẫu và điều tiếp theo cần được xác định là mối quan hệ ràng buộc giữa các biến này. Điều này cũng dễ hiểu, sau khi các thành phần tương tự được đưa vào bảng mạch bánh mì, mối quan hệ giữa chúng cần được xác định theo yêu cầu của mạch, sau đó được kết nối và hàn. Gọi hàm add_r1cs_constraint() của protoboard như sau để thêm r1cs_constraint dạng a*b=c vào pb. Cụ thể là r1cs_constraint(a, b,Các tham số trong c) phải thỏa mãn a * b = c. Không khó để hiểu mối quan hệ giữa mỗi phương trình và các ràng buộc theo các nhận xét.

// x*x = sym_1
pb.add_r1cs_constraint(r1cs_constraint(x, x, sym_1));
// sym_1 * x = y
pb.add_r1cs_constraint(r1cs_constraint(sym_1, x, y));
// y + x = sym_2
pb.add_r1cs_constraint(r1cs_constraint(y + x, 1, sym_2));
// sym_2 + 5 = ~out
pb.add_r1cs_constraint(r1cs_constraint(sym_2 + 5, 1, out));

Cho đến nay, các ràng buộc giữa các biến cũng đã được thêm vào và mạch cho mệnh đề đã được xây dựng. Hãy bước vào bước thứ hai của "bốn bước" được đề cập ở trên: sử dụng thuật toán tạo (G) để tạo các tham số công khai (pk và vk) cho đề xuất, tức là thiết lập đáng tin cậy. Bạn có thể lấy khóa chứng minh và khóa xác minh đã tạo thông qua keypair.pk và keypair.vk tương ứng.

const r1cs_constraint_system constraint_system = pb.get_constraint_system();
const r1cs_gg_ppzksnark_keypair keypair = r1cs_gg_ppzksnark_generator(constraint_system);

Chuyển sang bước thứ ba để tạo chứng chỉ. Đầu tiên cung cấp các giá trị cụ thể cho đầu vào công khai và nhân chứng. Không khó để thấy rằng x = 3, out = 35 là một nghiệm của phương trình ban đầu. Sau đó lần lượt gán giá trị cho x, out và từng biến trung gian.

pb.val(out) = 35;

pb.val(x) = 3;
pb.val(sym_1) = 9;
pb.val(y) = 27;
pb.val(sym_2) = 30;

Sau đó, chuyển các giá trị của đầu vào công khai và nhân chứng cho hàm chứng minh để chứng minh, có thể được truy cập thông qua pb.primary_input() và pb.auxiliary_input() tương ứng. Bằng chứng đã tạo được lưu với biến bằng chứng.

const r1cs_gg_ppzksnark_proof proof = r1cs_gg_ppzksnark_prover(keypair.pk, pb.primary_input(), pb.auxiliary_input());

Cuối cùng, chúng tôi xác minh bằng chứng bằng chức năng xác minh. Nếu xác minh = true, xác minh bằng chứng thành công.

bool verified = r1cs_gg_ppzksnark_verifier_strong_IC(keypair.vk, pb.primary_input(), proof);

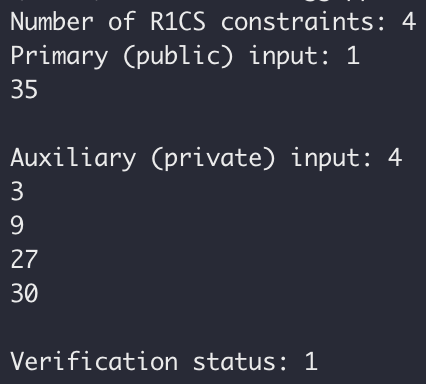
Từ đầu ra nhật ký, có thể thấy rằng kết quả xác minh là đúng, số ràng buộc R1CS là 4 và số đầu vào công khai và đầu vào riêng lần lượt là 1 và 4. Đầu ra nhật ký như mong đợi.

Trong các ứng dụng thực tế, việc thiết lập, chứng minh và xác minh đáng tin cậy sẽ được thực hiện bởi các vai trò khác nhau. Tác dụng cuối cùng là người chứng minh sẽ cung cấp cho người xác minh một bằng chứng ngắn và đầu vào công khai, và người xác minh có thể tự xác minh xem một mệnh đề có đúng hay không. Đối với ví dụ trước, có thể xác minh rằng người chứng minh biết một bí mật x để có thể thiết lập x^3 + x + 5 = out mà không cần biết nghiệm cụ thể x của phương trình.

Chỉ với vài chục dòng mã, bạn có thể dễ dàng thao tác với các kết quả nghiên cứu mới nhất về zk-SNARK trong giới học thuật.

5. Thực hành lại

Qua các ví dụ trên, chúng ta đã thấy tất cả các bước quan trọng để phát triển mạch zk-SNARKs bằng thư viện libsnark.

Bây giờ hãy củng cố nó bằng một ví dụ mới: Chứng minh rằng số nhỏ hơn 60 mà không tiết lộ kích thước của số bí mật.

Làm thế nào điều này có thể được thực hiện với một toán tử trong một chương trình thông thường được thể hiện dưới libsnark?

Khối lượng công việc và khó khăn chính của việc phát triển mạch zk-SNARKs là làm thế nào để mô tả "chính xác" tất cả các ràng buộc trong đề xuất bằng mã. Một khi mô tả không “chính xác” thì các ràng buộc hoặc bị bỏ sót hoặc viết sai, và nội dung mà mạch cuối muốn chứng minh sẽ khác xa với mệnh đề ban đầu. Các ví dụ trong phần trước chỉ liên quan đến phép nhân và phép cộng đơn giản, phù hợp với dạng cơ bản nhất của r1cs_constraint nên việc biểu diễn các ràng buộc tương đối dễ dàng. Ngoài ra, hầu hết tất cả các ràng buộc đều không trực quan lắm và người mới bắt đầu khó có thể mô tả chi tiết các ràng buộc một cách chính xác.

May mắn thay, libsnark đã triển khai rất nhiều tiện ích mạch cơ bản cho chúng tôi. Một số tiện ích được cung cấp theo tiện ích lib1 và tiện ích lib2 đã sẵn sàng để sử dụng. Trong số đó, gadgetlib1 được sử dụng phổ biến hơn và nó thu thập các phép tính băm bao gồm sha256, cây merkle, ghép nối và các triển khai mạch khác.

DangDangDang, so sánh_gadget trong gadgetlib1/gadgets/basic_gadgets.hpp chính xác là những gì chúng ta cần.

comparison_gadget(protoboard& pb,
const size_t n,
const pb_linear_combination &A,
const pb_linear_combination &B,
const pb_variable &less,
const pb_variable &less_or_eq,
const std::string &annotation_prefix="")

Tiện ích cần truyền vào nhiều tham số: n cho biết số chữ số, A và B là hai số được so sánh, less và less_or_eq dùng để đánh dấu mối quan hệ giữa hai số là "nhỏ hơn" hay "nhỏ hơn" hơn hoặc bằng”. Nguyên tắc triển khai tiện ích chỉ đơn giản là chuyển đổi phép so sánh giữa A và B thành 2^n + B - Biểu diễn theo bit. Việc triển khai cụ thể cũng sử dụng một số tiện ích cơ bản khác, có thể được chuyển qua so sánh_gadget::generate_r1cs_constraints() nghiên cứu.

Tại đây, bạn cần tạo các biến sau, kết nối x và max với pb và đặt giá trị tối đa thành 60, đại diện cho giới hạn trên của giá trị.

protoboard pb;

pb_variable x, max;
pb_variable less, less_or_eq;

x.allocate(pb, "x");
max.allocate(pb, "max");

pb.val(max)= 60;

Sử dụng compare_gadget để tạo cmp, điền các tham số trước đó và gọi phương thức generate_r1cs_constraints() đi kèm với tiện ích. Đồng thời, thêm một ràng buộc khác, yêu cầu ít hơn * 1 = 1, nghĩa là ít hơn phải đúng.

comparison_gadget cmp(pb, 10, x, max, less, less_or_eq, "cmp");
cmp.generate_r1cs_constraints();
pb.add_r1cs_constraint(r1cs_constraint(less, 1, FieldT::one()));

Nhập nhân chứng (giá trị bí mật x), giả sử x = 18. Ở đây cũng cần gọi phương thức generate_r1cs_witness của so sánh_gadget.

// Add witness values
pb.val(x) = 18; // secret
cmp.generate_r1cs_witness();

Phần còn lại phù hợp với ví dụ trước, nghĩa là có thể chứng minh rằng một số nhỏ hơn 60 mà không tiết lộ kích thước của số bí mật. Theo cách tương tự, một "chứng minh phạm vi" giới hạn giá trị tối đa và tối thiểu của giá trị được triển khai.

Với sự trợ giúp của một thư viện cơ bản mạnh mẽ, chúng tôi đã đạt được các yêu cầu về bằng chứng với mã ngắn hơn.

6. What's NEXT?

Sau khi đọc phần này, tôi tin rằng mọi người đã hiểu sơ bộ về cách sử dụng libsnark và phát triển mạch zk-SNARK.

Bạn có thể đã phát hiện ra rằng libsnark sử dụng tương đối đơn giản và trọng tâm thực sự là phát triển mạch zk-SNARK. Như đã đề cập trước đó, mã phải được sử dụng để mô tả "chính xác" tất cả các ràng buộc trong mệnh đề cần chứng minh. Các ràng buộc "thiếu" hoặc "viết sai" sẽ làm cho nội dung của chứng minh rất khác so với ý định ban đầu, làm cho chứng minh trở nên vô nghĩa .

Cách chuyển đổi logic kinh doanh thực tế thành mã mạch zk-SNARKs một cách chính xác và hiệu quả chính là điều mà các nhà phát triển của chúng tôi cần liên tục nghiên cứu và thực hành.

May mắn thay, chúng tôi đã có cơ sở chứng minh libsnark và chúng tôi có thể dễ dàng sửa đổi và thêm mã để thử.

Cho dù việc thực hiện mạch phức tạp đến đâu, nó được hình thành bằng cách kết hợp và đóng gói từng "linh kiện mạch" đơn giản hơn. Do đó, thư viện cơ bản đi kèm với libsnark là một tài liệu học tập rất quan trọng - không chỉ để học cách sử dụng chúng mà còn để nghiên cứu các nguyên tắc thực hiện của chúng.

Chúng ta cũng có thể hiểu cách áp dụng ZKP vào kinh doanh thực tế bằng cách đọc mạch triển khai của các dự án khác, chẳng hạn như HarryR'sethsnarks-miximusvà Loopringprotocol3-circuits. Từ những dự án này, bạn có thể học cách thiết kế và phát triển các mạch quy mô lớn hơn, cũng như các chi tiết tối ưu hóa thiết kế khác nhau liên quan đến hiệu suất mạch, đồng thời hiểu sâu hơn về quy mô của các ràng buộc mạch.

Đồng thời, mời mọi người tiếp tục chú ý theo dõi các bài viết tiếp theo của "Zero-knowledge proof Learn by Coding: libsnark series" của Ambi Lab. Lần tới chúng ta sẽ thử kết hợp zk-SNARK với hợp đồng thông minh, phát triển mô-đun mạch, các trường hợp triển khai libsnark phức tạp hơn, Các hố dễ mắc phải trong quá trình phát triển mạch sẽ được thảo luận thêm.

7. Phụ lục

main.cpp

Ví dụ đầu tiên, main.cpp, gọi mã mẫu của ví dụ chính thức về libsnark. Thông qua ví dụ này, bạn có thể hiểu quy trình sử dụng cơ bản và các chức năng chính của libsnark.

#include
#include
#include
#include

using namespace libsnark;

/**
* The code below provides an example of all stages of running a R1CS GG-ppzkSNARK.
*
* Of course, in a real-life scenario, we would have three distinct entities,
* mangled into one in the demonstration below. The three entities are as follows.
* (1) The "generator", which runs the ppzkSNARK generator on input a given
* constraint system CS to create a proving and a verification key for CS.
* (2) The "prover", which runs the ppzkSNARK prover on input the proving key,
* a primary input for CS, and an auxiliary input for CS.
* (3) The "verifier", which runs the ppzkSNARK verifier on input the verification key,
* a primary input for CS, and a proof.
*/
template
bool run_r1cs_gg_ppzksnark(const r1cs_example > &example)
{
libff::print_header("R1CS GG-ppzkSNARK Generator");
r1cs_gg_ppzksnark_keypair keypair = r1cs_gg_ppzksnark_generator(example.constraint_system);
printf("\n"); libff::print_indent(); libff::print_mem("after generator");

libff::print_header("Preprocess verification key");
r1cs_gg_ppzksnark_processed_verification_key pvk = r1cs_gg_ppzksnark_verifier_process_vk(keypair.vk);

libff::print_header("R1CS GG-ppzkSNARK Prover");
r1cs_gg_ppzksnark_proof proof = r1cs_gg_ppzksnark_prover(keypair.pk, example.primary_input, example.auxiliary_input);
printf("\n"); libff::print_indent(); libff::print_mem("after prover");

libff::print_header("R1CS GG-ppzkSNARK Verifier");
const bool ans = r1cs_gg_ppzksnark_verifier_strong_IC(keypair.vk, example.primary_input, proof);
printf("\n"); libff::print_indent(); libff::print_mem("after verifier");
printf("* The verification result is: %s\n", (ans ? "PASS" : "FAIL"));

libff::print_header("R1CS GG-ppzkSNARK Online Verifier");
const bool ans2 = r1cs_gg_ppzksnark_online_verifier_strong_IC(pvk, example.primary_input, proof);
assert(ans == ans2);

return ans;
}

template
void test_r1cs_gg_ppzksnark(size_t num_constraints, size_t input_size)
{
r1cs_example > example = generate_r1cs_example_with_binary_input >(num_constraints, input_size);
const bool bit = run_r1cs_gg_ppzksnark(example);
assert(bit);
}

int main () {
default_r1cs_gg_ppzksnark_pp::init_public_params();
test_r1cs_gg_ppzksnark(1000, 100);

return 0;
}

test.cpp

Ví dụ thứ hai test.cpp. Ví dụ này cho thấy cách sử dụng libsnark để xây dựng mạch đơn giản nhất.

#include
#include
#include

using namespace libsnark;
using namespace std;

int main () {
typedef libff::Fr FieldT;

// Initialize the curve parameters
default_r1cs_gg_ppzksnark_pp::init_public_params();

// Create protoboard
protoboard pb;

// Define variables
pb_variable x;
pb_variable sym_1;
pb_variable y;
pb_variable sym_2;
pb_variable out;

// Allocate variables to protoboard
// The strings (like "x") are only for debugging purposes
out.allocate(pb, "out");
x.allocate(pb, "x");
sym_1.allocate(pb, "sym_1");
y.allocate(pb, "y");
sym_2.allocate(pb, "sym_2");

// This sets up the protoboard variables
// so that the first one (out) represents the public
// input and the rest is private input
pb.set_input_sizes(1);

// Add R1CS constraints to protoboard

// x*x = sym_1
pb.add_r1cs_constraint(r1cs_constraint(x, x, sym_1));

// sym_1 * x = y
pb.add_r1cs_constraint(r1cs_constraint(sym_1, x, y));

// y + x = sym_2
pb.add_r1cs_constraint(r1cs_constraint(y + x, 1, sym_2));

// sym_2 + 5 = ~out
pb.add_r1cs_constraint(r1cs_constraint(sym_2 + 5, 1, out));

const r1cs_constraint_system constraint_system = pb.get_constraint_system();

// generate keypair
const r1cs_gg_ppzksnark_keypair keypair = r1cs_gg_ppzksnark_generator(constraint_system);

// Add public input and witness values
pb.val(out) = 35;

pb.val(x) = 3;
pb.val(sym_1) = 9;
pb.val(y) = 27;
pb.val(sym_2) = 30;

// generate proof
const r1cs_gg_ppzksnark_proof proof = r1cs_gg_ppzksnark_prover(keypair.pk, pb.primary_input(), pb.auxiliary_input());

// verify
bool verified = r1cs_gg_ppzksnark_verifier_strong_IC(keypair.vk, pb.primary_input(), proof);

cout << "Number of R1CS constraints: " << constraint_system.num_constraints() << endl;
cout << "Primary (public) input: " << pb.primary_input() << endl;
cout << "Auxiliary (private) input: " << pb.auxiliary_input() << endl;
cout << "Verification status: " << verified << endl;
}