LUCIDA:如何利用多因子策略构建强大的加密资产投资组合(因子有效性检验篇)
คำนำ
ต่อจากหนังสือเล่มที่แล้ว เราได้ตีพิมพ์บทความสองบทความในชุดบทความเกี่ยวกับ การสร้างพอร์ตโฟลิโอสินทรัพย์ดิจิทัลที่มีประสิทธิภาพโดยใช้แบบจำลองหลายปัจจัย:“พื้นฐานทางทฤษฎี”、“การประมวลผลข้อมูลล่วงหน้า”
นี่คือบทความที่สาม: การทดสอบความถูกต้องของปัจจัย
หลังจากกำหนดค่าปัจจัยเฉพาะแล้ว จำเป็นต้องดำเนินการทดสอบความถูกต้องของปัจจัยและปัจจัยคัดกรองที่ตรงตามข้อกำหนดด้านนัยสำคัญ ความเสถียร ความน่าเบื่อ และอัตราผลตอบแทนก่อน การทดสอบความถูกต้องของปัจจัยทำได้โดยการวิเคราะห์ความสัมพันธ์ระหว่างปัจจัย มูลค่าของงวดปัจจุบันและความสัมพันธ์ของอัตราผลตอบแทนที่คาดหวังเพื่อกำหนดความถูกต้องของปัจจัย โดยทั่วไปมี 3 วิธีแบบคลาสสิก:
วิธี IC/IR: ค่า IC/IR คือค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างค่าตัวประกอบและผลตอบแทนที่คาดหวัง ยิ่งค่าปัจจัยมาก ประสิทธิภาพก็จะยิ่งดีขึ้น
ค่า T (วิธีการถดถอย): ค่า T สะท้อนถึงความสำคัญของสัมประสิทธิ์หลังจากการถดถอยเชิงเส้นของผลตอบแทนของงวดถัดไปจากค่าตัวประกอบของงวดปัจจุบัน โดยการเปรียบเทียบว่าค่าสัมประสิทธิ์การถดถอยผ่านการทดสอบ t หรือไม่ เราสามารถตัดสินการมีส่วนร่วมของ ค่าตัวประกอบของงวดปัจจุบันเทียบกับผลตอบแทนของงวดถัดไป โดยทั่วไปจะใช้ในแบบจำลองการถดถอยหลายตัวแปร (เช่น หลายปัจจัย)
วิธีการทดสอบย้อนกลับแบบลำดับชั้น: วิธีการทดสอบย้อนกลับแบบลำดับชั้นจะแบ่งโทเค็นตามค่าปัจจัย จากนั้นคำนวณอัตราผลตอบแทนของโทเค็นแต่ละชั้นเพื่อกำหนดความซ้ำซ้อนของปัจจัยต่างๆ
1. กฎหมาย IC/IR
(1) คำจำกัดความของ IC/IR
IC: ค่าสัมประสิทธิ์ข้อมูล ซึ่งแสดงถึงความสามารถของปัจจัยในการทำนายผลตอบแทนของโทเค็น ค่า IC ของช่วงเวลาหนึ่งคือค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างค่าตัวประกอบของช่วงเวลาปัจจุบันและอัตราผลตอบแทนของช่วงเวลาถัดไป
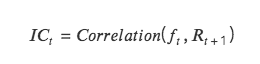

ยิ่ง IC ใกล้ 1 มากเท่าใด ความสัมพันธ์เชิงบวกระหว่างค่าปัจจัยและอัตราผลตอบแทนของงวดถัดไปก็จะยิ่งแข็งแกร่งขึ้นเท่านั้น IC= 1 หมายความว่าการเลือกสกุลเงินของปัจจัยนั้นแม่นยำ 100% ซึ่งสอดคล้องกับโทเค็นที่มีคะแนนอันดับสูงสุด โทเค็นที่เลือกจะถูกใช้ในรอบการปรับตำแหน่งถัดไป , เพิ่มขึ้นมากที่สุด;
ยิ่ง IC ใกล้ -1 มากเท่าใด ความสัมพันธ์เชิงลบระหว่างค่าปัจจัยและอัตราผลตอบแทนในช่วงถัดไปก็จะยิ่งแข็งแกร่งขึ้นเท่านั้น หาก IC=-1 หมายความว่าโทเค็นที่มีอันดับสูงสุดจะมีการลดลงมากที่สุดในช่วงถัดไป วงจรการปรับสมดุลซึ่งเป็นการผกผันที่สมบูรณ์ ดัชนี;
ถ้า IC ใกล้ 0 มากขึ้น หมายความว่าความสามารถในการคาดการณ์ของปัจจัยนั้นอ่อนมาก ซึ่งบ่งชี้ว่าปัจจัยนั้นไม่มีความสามารถในการคาดการณ์สำหรับโทเค็น
IR: อัตราส่วนข้อมูลซึ่งแสดงถึงความสามารถของปัจจัยในการรับอัลฟ่าที่เสถียร IR คือค่าเฉลี่ย IC ของทุกงวดหารด้วยค่าเบี่ยงเบนมาตรฐานของ IC ของทุกงวด
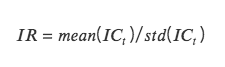
เมื่อค่าสัมบูรณ์ของ IC มากกว่า 0.05 (0.02) ความสามารถในการเลือกหุ้นของปัจจัยจะแข็งแกร่ง เมื่อ IR มากกว่า 0.5 ปัจจัยนี้มีความสามารถที่แข็งแกร่งในการได้รับผลตอบแทนส่วนเกินอย่างคงที่
(2) วิธีคำนวณไอซี
IC ปกติ (สหสัมพันธ์เพียร์สัน): คำนวณค่าสัมประสิทธิ์สหสัมพันธ์เพียร์สัน ซึ่งเป็นค่าสัมประสิทธิ์สหสัมพันธ์แบบคลาสสิกที่สุด อย่างไรก็ตาม วิธีการคำนวณนี้มีข้อสันนิษฐานหลายประการ เช่น ข้อมูลมีความต่อเนื่อง มีการกระจายแบบปกติ ตัวแปรทั้งสองเป็นไปตามความสัมพันธ์เชิงเส้น เป็นต้น
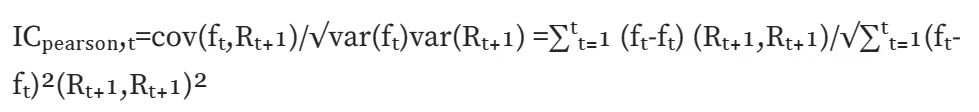
อันดับ IC (สัมประสิทธิ์สหสัมพันธ์อันดับของสเปียร์แมน): คำนวณค่าสัมประสิทธิ์สหสัมพันธ์อันดับของสเปียร์แมน อันดับแรกเรียงลำดับตัวแปรทั้งสอง จากนั้นคำนวณค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สันตามผลลัพธ์ที่เรียงลำดับค่าสัมประสิทธิ์สหสัมพันธ์อันดับของสเปียร์แมนจะประเมินความสัมพันธ์แบบโมโนโทนิกระหว่างตัวแปรสองตัว และได้รับผลกระทบจากค่าผิดปกติของข้อมูลน้อยกว่าเนื่องจากจะถูกแปลงเป็นค่าที่เรียงลำดับค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันจะประเมินความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว ซึ่งไม่เพียงแต่มีข้อกำหนดเบื้องต้นบางประการสำหรับข้อมูลต้นฉบับเท่านั้น แต่ยังได้รับผลกระทบอย่างมากจากค่าผิดปกติของข้อมูลอีกด้วย ในการคำนวณในชีวิตจริง การค้นหาอันดับ IC จะมีความสม่ำเสมอมากกว่า
(3) การใช้รหัสวิธี IC/IR
สร้างรายการค่าวันที่และเวลาที่ไม่ซ้ำกันโดยเรียงลำดับวันที่และเวลาจากน้อยไปหามาก - บันทึกวันที่ปรับสมดุลใหม่ def choosedate(dateList, รอบ)
class TestAlpha(object):
def __init__(self, ini_data):
self.ini_data = ini_data
def chooseDate(self, cycle, start_date, end_date):
'''
cycle: day, month, quarter, year
df: กรอบข้อมูลดั้งเดิม df, การประมวลผลคอลัมน์วันที่
'''
chooseDate = []
dateList = sorted(self.ini_data[self.ini_data['date'].between(start_date, end_date)]['date'].drop_duplicates().values)
dateList = pd.to_datetime(dateList)
for i in range(len(dateList)-1):
if getattr(dateList[i], cycle) != getattr(dateList[i + 1 ], cycle):
chooseDate.append(dateList[i])
chooseDate.append(dateList[-1 ])
chooseDate = [date.strftime('%Y-%m-%d') for date in chooseDate]
return chooseDate
def ICIR(self, chooseDate, factor):
# 1. ขั้นแรกให้แสดง IC ของวันที่ปรับตำแหน่งแต่ละตำแหน่ง นั่นคือ ICT
testIC = pd.DataFrame(index=chooseDate, columns=['normalIC','rankIC'])
dfFactor = self.ini_data[self.ini_data['date'].isin(chooseDate)][['date','name','price', factor]]
for i in range(len(chooseDate)-1):
# ( 1) normalIC
X = dfFactor[dfFactor['date'] == chooseDate[i]][['date','name','price', factor]].rename(columns={'price':'close 0'})
Y = pd.merge(X, dfFactor[dfFactor['date'] == chooseDate[i+ 1 ]][['date','name','price']], on=['name']).rename(columns={'price':'close 1'})
Y['returnM'] = (Y['close 1'] - Y['close 0']) / Y['close 0']
Yt = np.array(Y['returnM'])
Xt = np.array(Y[factor])
Y_mean = Y['returnM'].mean()
X_mean = Y[factor].mean()
num = np.sum((Xt-X_mean)*(Yt-Y_mean))
den = np.sqrt(np.sum((Xt-X_mean)** 2)*np.sum((Yt-Y_mean)** 2))
normalIC = num / den # pearson correlation
# ( 2) rankIC
Yr = Y['returnM'].rank()
Xr = Y[factor].rank()
rankIC = Yr.corr(Xr)
testIC.iloc[i] = normalIC, rankIC
testIC =testIC[:-1 ]
# 2. จาก ICT ให้ค้นหา [IC_Mean, IC_Std,IR,IC<0 สัดส่วน - ทิศทางปัจจัย,-IC->สัดส่วน 0.05]
'''
ICmean: |IC|>0.05,ปัจจัยมีความสามารถสูงในการเลือกเหรียญ และค่าปัจจัยมีความสัมพันธ์สูงกับอัตราผลตอบแทนของงวดถัดไป -เข้าใจแล้ว-<0.05,ความสามารถในการเลือกสกุลเงินของปัจจัยนั้นอ่อนแอ และความสัมพันธ์ระหว่างค่าปัจจัยและอัตราผลตอบแทนของงวดถัดไปต่ำ
IR: |IR|>0.5,ความสามารถในการเลือกสกุลเงินของปัจจัยนั้นแข็งแกร่งและค่า IC ค่อนข้างคงที่ -ไออาร์-<0.5,ค่า IR น้อยเกินไปและปัจจัยไม่มีประสิทธิผลมากนัก หากเข้าใกล้ 0 ถือว่าไม่ถูกต้องโดยทั่วไป
IClZero (IC น้อยกว่าศูนย์): IC<0 คิดเป็นเกือบครึ่งหนึ่ง -> แฟกเตอร์เป็นกลาง IC>0 เกินมากกว่าครึ่งซึ่งเป็นปัจจัยลบ กล่าวคือ เมื่อค่าแฟกเตอร์เพิ่มขึ้น อัตราผลตอบแทนจะลดลง
ICALzpF(IC abs large than zero poin five): |IC|>อัตราส่วน 0.05 อยู่ในระดับสูง บ่งชี้ว่าปัจจัยส่วนใหญ่มีประสิทธิผล
'''
IR = testIC.mean()/testIC.std()
IClZero = testIC[testIC<0 ].count()/testIC.count()
ICALzpF = testIC[abs(testIC)>0.05 ].count()/testIC.count()
combined =pd.concat([testIC.mean(), testIC.std(), IR, IClZero, ICALzpF], axis= 1)
combined.columns = ['ICmean','ICstd','IR','IClZero','ICALzpF']
# 3.IC แผนภูมิสะสมของ IC ในช่วงระยะเวลาการปรับสมดุล
print("Test IC Table:")
print(testIC)
print("Result:")
print('normal Skewness:', combined['normalIC'].skew(),'rank Skewness:', combined['rankIC'].skew())
print('normal Skewness:', combined['normalIC'].kurt(),'rank Skewness:', combined['rankIC'].kurt())
return combined, testIC.cumsum().plot()
2. การทดสอบค่า T (วิธีถดถอย)
วิธีค่า T ยังทดสอบความสัมพันธ์ระหว่างค่าตัวประกอบของงวดปัจจุบันกับอัตราผลตอบแทนของงวดถัดไป แต่จะแตกต่างจากวิธี ICIR ในการวิเคราะห์ความสัมพันธ์ระหว่างทั้งสอง วิธีค่า t ใช้อัตราของงวดถัดไปของ ส่งกลับเป็นตัวแปรตาม Y และค่าตัวประกอบของงวดปัจจุบันเป็นตัวแปรอิสระ X สำหรับการถดถอย X ให้ทำการทดสอบ t กับค่าสัมประสิทธิ์การถดถอยของค่าตัวประกอบการถดถอยเพื่อทดสอบว่าค่าดังกล่าวแตกต่างอย่างมีนัยสำคัญจาก 0 หรือไม่ นั่นคือว่า ปัจจัยงวดปัจจุบันส่งผลต่ออัตราผลตอบแทนของงวดถัดไป
สาระสำคัญของวิธีนี้คือการแก้แบบจำลองการถดถอยแบบสองตัวแปรโดยมีสูตรเฉพาะดังนี้
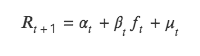

(1) ทฤษฎีวิธีถดถอย

(2) การใช้รหัสวิธีการถดถอย
def regT(self, chooseDate, factor, return_ 24 h):
testT = pd.DataFrame(index=chooseDate, columns=['coef','T'])
for i in range(len(chooseDate)-1):
X = self.ini_data[self.ini_data['date'] == chooseDate[i]][factor].values
Y = self.ini_data[self.ini_data['date'] == chooseDate[i+ 1 ]][return_ 24 h].values
b, intc = np.polyfit(X, Y,1) # ความชัน
ut = Y - (b * X + intc)
# ค้นหาค่า t = (\hat{b} - b) / se(b)
n = len(X)
dof = n - 2 # องศาอิสระ
std_b = np.sqrt(np.sum(ut** 2) / dof)
t_stat = b / std_b
testT.iloc[i] = b, t_stat
testT = testT[:-1 ]
testT_mean = testT['T'].abs().mean()
testT L1 96 = len(testT[testT['T'].abs() > 1.96 ]) / len(testT)
print('testT_mean:', testT_mean)
print(สัดส่วนของค่า T ที่มากกว่า 1.96:, testT L1 96)
return testT
3. วิธีการทดสอบย้อนหลังแบบแบ่งชั้น
การแบ่งชั้นหมายถึงการแบ่งชั้นโทเค็นทั้งหมด และการทดสอบย้อนกลับหมายถึงการคำนวณอัตราการส่งคืนของแต่ละเลเยอร์ของการรวมโทเค็น
(1) การแบ่งชั้น
ขั้นแรก รับค่าตัวประกอบที่สอดคล้องกับพูลโทเค็น และเรียงลำดับโทเค็นตามค่าตัวประกอบ เรียงลำดับจากน้อยไปมาก นั่นคือค่าที่มีค่าตัวประกอบน้อยกว่าจะถูกจัดอันดับเป็นอันดับแรก และโทเค็นจะถูกแบ่งเท่าๆ กันตามการเรียงลำดับ ค่าตัวประกอบของโทเค็นเลเยอร์ 0 มีค่าน้อยที่สุด และค่าตัวประกอบของโทเค็นเลเยอร์ 9 มีค่ามากที่สุด
ตามทฤษฎีแล้ว การแบ่งเท่ากัน หมายถึงการแบ่งจำนวนโทเค็นให้เท่าๆ กัน กล่าวคือ จำนวนโทเค็นในแต่ละเลเยอร์จะเท่ากัน ซึ่งสามารถทำได้ด้วยความช่วยเหลือของควอนไทล์ ในความเป็นจริง จำนวนโทเค็นทั้งหมดไม่จำเป็นต้องเป็นผลคูณของจำนวนเลเยอร์ กล่าวคือ จำนวนโทเค็นในแต่ละเลเยอร์ไม่จำเป็นต้องเท่ากัน
(2) การทดสอบย้อนกลับ
หลังจากแบ่งโทเค็นออกเป็น 10 กลุ่มตามลำดับค่าตัวประกอบจากน้อยไปหามาก ให้เริ่มคำนวณอัตราการส่งคืนของการรวมโทเค็นแต่ละรายการ ขั้นตอนนี้ถือว่าโทเค็นของแต่ละเลเยอร์เป็นพอร์ตการลงทุน (โทเค็นที่มีอยู่ในการรวมโทเค็นของแต่ละเลเยอร์จะเปลี่ยนแปลงในช่วงระยะเวลาการทดสอบย้อนกลับที่แตกต่างกัน) และคำนวณมูลค่าโดยรวมของพอร์ตโฟลิโออัตราผลตอบแทนงวดถัดไป. ICIR และค่า t วิเคราะห์ค่าตัวประกอบปัจจุบันและอัตราผลตอบแทนโดยรวมในช่วงถัดไปแต่การทดสอบย้อนหลังแบบเป็นชั้นจำเป็นต้องมีการคำนวณอัตราผลตอบแทนพอร์ตโฟลิโอแบบแบ่งชั้นสำหรับแต่ละวันซื้อขายในช่วงระยะเวลาการทดสอบย้อนหลัง. เนื่องจากมีช่วงการทดสอบย้อนหลังหลายช่วงซึ่งมีหลายช่วง จึงจำเป็นต้องมีการแบ่งชั้นและการทดสอบย้อนกลับในแต่ละช่วง สุดท้าย อัตราผลตอบแทนโทเค็นของแต่ละเลเยอร์จะถูกคูณสะสมเพื่อคำนวณอัตราผลตอบแทนสะสมของการรวมโทเค็น
ตามหลักการแล้ว สำหรับปัจจัยที่ดี กลุ่ม 9 มีผลตอบแทนจากเส้นโค้งสูงสุด และกลุ่ม 0 มีผลตอบแทนจากเส้นโค้งต่ำที่สุด
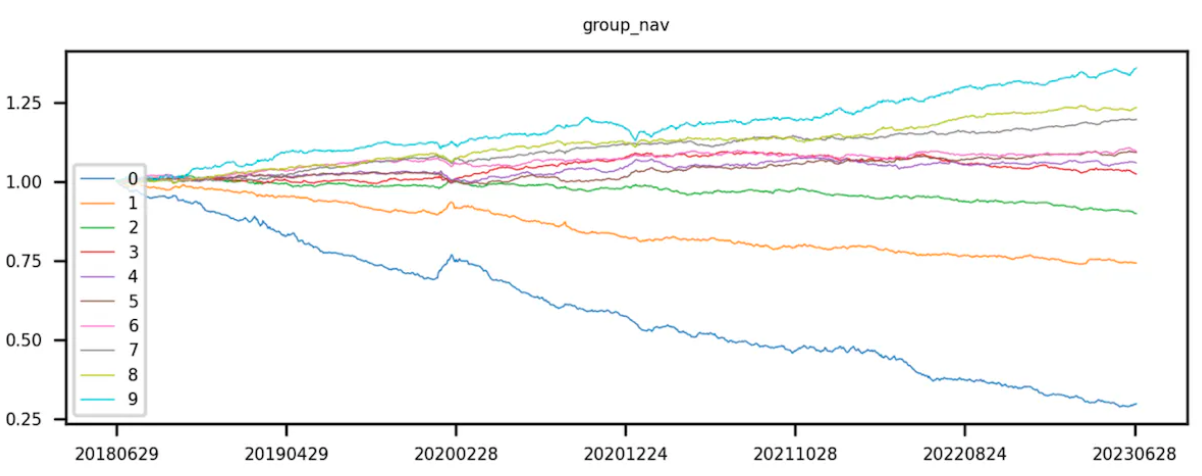
เส้นโค้งสำหรับกลุ่ม 9 ลบกลุ่ม 0 (เช่น ผลตอบแทนระยะสั้น-ระยะยาว) กำลังเพิ่มขึ้นอย่างซ้ำซากจำเจ
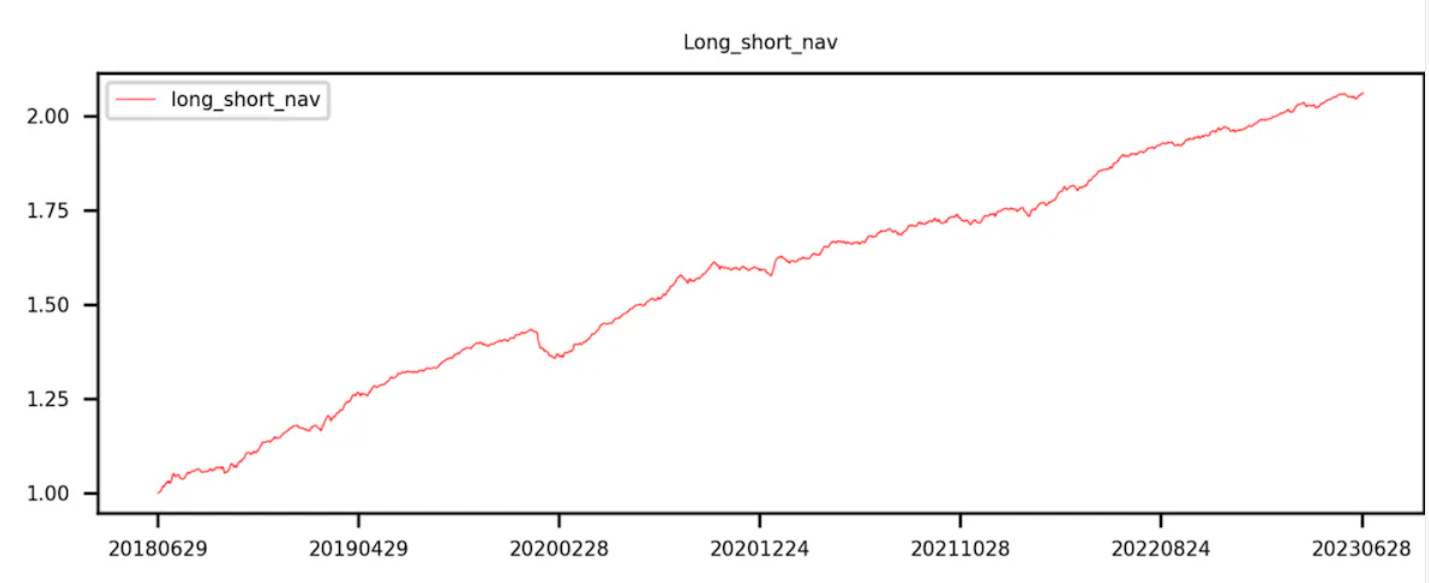
(3) การใช้โค้ดของวิธีการทดสอบย้อนกลับแบบลำดับชั้น
def layBackTest(self, chooseDate, factor):
f = {}
returnM = {}
for i in range(len(chooseDate)-1):
df 1 = self.ini_data[self.ini_data['date'] == chooseDate[i]].rename(columns={'price':'close 0'})
Y = pd.merge(df 1, self.ini_data[self.ini_data['date'] == chooseDate[i+ 1 ]][['date','name','price']], left_on=['name'], right_on=['name']).rename(columns={'price':'close 1'})
f[i] = Y[factor]
returnM[i] = Y['close 1'] / Y['close 0'] -1
labels = ['0','1','2','3','4','5','6','7','8','9']
res = pd.DataFrame(index=['0','1','2','3','4','5','6','7','8','9','LongShort'])
res[chooseDate[ 0 ]] = 1
for i in range(len(chooseDate)-1):
dfM = pd.DataFrame({'factor':f[i],'returnM':returnM[i]})
dfM['group'] = pd.qcut(dfM['factor'], 10, labels=labels)
dfGM = dfM.groupby('group').mean()[['returnM']]
dfGM.loc[LongShort] = dfGM.loc[0]- dfGM.loc[9]res[chooseDate[i+ 1 ]] = res[chooseDate[ 0 ]] * ( 1 + dfGM[returnM ]) data = pd.DataFrame({ผลตอบแทนสะสมตามลำดับชั้น:res.iloc[: 10,-1],กลุ่ม:[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ]})
df 3 = data.corr()
print("Correlation Matrix:")
print(df 3)
return res.T.plot(title='Group backtest net worth curve')



