คำนำ

คำนำ

เทคโนโลยีการพิสูจน์ความรู้ที่ไม่มีความรู้ในการเข้ารหัสมีแอปพลิเคชันที่หลากหลายในโลกของ web3 รวมถึงการประมวลผลส่วนตัว zkRollup และอื่นๆ ในหมู่พวกเขา FOAKS ที่ใช้โดยโครงการเลเยอร์ 2 FOX เป็นอัลกอริทึมการพิสูจน์ความรู้ที่ไม่มีศูนย์ ในบรรดาชุดแอปพลิเคชันที่กล่าวถึงข้างต้น คุณลักษณะสองประการมีความสำคัญอย่างยิ่งสำหรับอัลกอริทึมการพิสูจน์ด้วยความรู้เป็นศูนย์ นั่นคือ ประสิทธิภาพและการโต้ตอบของอัลกอริทึม

ความสำคัญของประสิทธิภาพของอัลกอริทึมนั้นชัดเจนในตัวเอง อัลกอริทึมที่มีประสิทธิภาพสามารถลดรันไทม์ของระบบได้อย่างมาก จึงช่วยลดเวลาแฝงของไคลเอนต์และปรับปรุงประสบการณ์และประสิทธิภาพของผู้ใช้อย่างมีนัยสำคัญ นี่เป็นเหตุผลสำคัญที่ FOAKS มุ่งมั่นที่จะบรรลุเวลาพิสูจน์เชิงเส้น

ในทางกลับกัน จากมุมมองของวิทยาการเข้ารหัสลับ การออกแบบระบบพิสูจน์ความรู้ที่ไม่มีความรู้มักจะอาศัยปฏิสัมพันธ์หลายรอบระหว่างผู้พิสูจน์และผู้ตรวจสอบ ตัวอย่างเช่น ในเรื่อง "Zero-Knowledge Cave" ที่ใช้ในบทความวิทยาศาสตร์ยอดนิยมหลายบทความที่แนะนำการพิสูจน์ที่ไม่มีความรู้ การพิสูจน์ให้เป็นจริงนั้นขึ้นอยู่กับการส่งข้อมูลและการโต้ตอบหลายรอบระหว่างอาลีบาบา (ผู้พิสูจน์) และผู้รายงาน ( ผู้ตรวจสอบ) แต่ในความเป็นจริง ในหลาย ๆ สถานการณ์ของแอปพลิเคชัน การพึ่งพาการโต้ตอบจะทำให้ระบบไม่พร้อมใช้งานอีกต่อไป หรือเพิ่มความล่าช้าอย่างมาก เช่นเดียวกับในระบบ zkRollup เราคาดหวังว่าผู้พิสูจน์ (นั่นคือโฟลเดอร์ใน FOX) จะสามารถคำนวณค่าการพิสูจน์ที่ถูกต้องในเครื่องโดยไม่ต้องขึ้นอยู่กับการโต้ตอบกับผู้ตรวจสอบ

ชื่อระดับแรก

ความท้าทายในการพิสูจน์ความรู้เป็นศูนย์

อัลกอริธึมการพิสูจน์ด้วยความรู้เป็นศูนย์ได้รับความนิยมอย่างมากจากการแพร่กระจายของแอปพลิเคชัน ในช่วงไม่กี่ปีที่ผ่านมา อัลกอริทึมต่างๆ เช่น FOAKS, Orion และ zk-stark ก็ถือกำเนิดขึ้นเช่นกัน ตรรกะการพิสูจน์หลักของอัลกอริทึมเหล่านี้ เช่นเดียวกับโปรโตคอล sigma รุ่นแรกๆ ในด้านการเข้ารหัส นั่นคือ ผู้พิสูจน์ (Prover) ก่อนส่งค่าหนึ่งไปยังผู้ตรวจสอบ (Verifier) ​​และผู้ตรวจสอบจะสร้างความท้าทาย (Challenge) ผ่าน ตัวเลขสุ่มในท้องถิ่น ค่า Challenge ที่สร้างขึ้นแบบสุ่มจะถูกส่งไปยังผู้พิสูจน์และผู้พิสูจน์จำเป็นต้องมีความรู้จริงเพื่อตอบกลับโดยมีโอกาสสูงที่จะผ่านผู้ตรวจสอบ ตัวอย่างเช่นในถ้ำที่ไม่มีความรู้นักข่าวโยนเหรียญและบอกให้อาลีบาบาออกมาจากซ้ายหรือขวา "ซ้ายและขวา" นี่คือความท้าทายของอาลีบาบาให้ออกไปในทิศทางที่กำหนดมิฉะนั้นจะมี จะมีโอกาสล้มเหลวเพียงครึ่งเดียว

ที่นี่เราสังเกตเห็นว่าการสร้างความท้าทายเป็นขั้นตอนที่สำคัญ มีข้อกำหนดสองข้อ คือ สุ่มและคาดเดาไม่ได้โดยผู้พิสูจน์ ประการแรก การสุ่มรับประกันคุณสมบัติความน่าจะเป็นของมัน ประเด็นที่สอง คือ ถ้าผู้พิสูจน์สามารถทำนายค่าความท้าทายได้ แสดงว่าความปลอดภัยของโปรโตคอลเสีย ผู้พิสูจน์สามารถผ่านการตรวจสอบได้โดยไม่ต้องมีความรู้ การเปรียบเทียบสามารถดำเนินต่อไปได้ ถ้าอาลีบาบาสามารถคาดเดาได้ว่านักข่าวถามเขาในด้านใด ถึงจะออกมาก็เข้าได้ แม้ไม่มีคาถา ก็สามารถเข้าฝั่งนั้นล่วงหน้าได้ และผลปรากฏว่า ผ่านข้อตกลงได้

ชื่อระดับแรก

ฟังก์ชันแฮช

ชื่อของฟังก์ชันแฮชอาจไม่คุ้นเคยสำหรับเรา ไม่ว่าจะเป็นปัญหาทางคณิตศาสตร์ของการขุดใน Bitcoin Consensus Protocol POW หรือการบีบอัดจำนวนข้อมูล การสร้างรหัสยืนยันข้อความ ฯลฯ ก็มีฟังก์ชันแฮช ในบรรดาโปรโตคอลต่างๆ ที่กล่าวถึงข้างต้น มีการใช้คุณสมบัติต่างๆ ของฟังก์ชันแฮชจริง

โดยเฉพาะอย่างยิ่ง คุณสมบัติของฟังก์ชันแฮชที่ปลอดภัยมีดังต่อไปนี้:

ความสามารถในการบีบอัด: ฟังก์ชันแฮชที่กำหนดสามารถบีบอัดข้อความที่มีความยาวเท่าใดก็ได้ให้มีความยาวคงที่

ประสิทธิภาพ: ด้วยอินพุต x ทำให้ง่ายต่อการคำนวณเอาต์พุต h(x)

การป้องกันการชนกัน: ให้อินพุต x 1 เป็นการยากที่จะหาอินพุตอื่น x 2 , x 1 x 2 , h(x 1 ) = h(x 2 )

โปรดทราบว่าหากฟังก์ชันแฮชตอบสนองการต้านทานการชนกัน ฟังก์ชันนั้นจะต้องเป็นไปตามคุณสมบัติทางเดียว กล่าวคือ เมื่อให้เอาต์พุต y การหาค่า x ที่พึงพอใจ h(x) = y จะทำได้ยาก ในวิทยาการเข้ารหัสลับ เป็นไปไม่ได้ที่จะสร้างฟังก์ชันที่ตรงตามคุณสมบัติทางเดียวในทางทฤษฎี แต่โดยพื้นฐานแล้วฟังก์ชันแฮชสามารถถือเป็นฟังก์ชันทางเดียวในการใช้งานจริงได้

ชื่อระดับแรก

Fiat-Shamir ฮิวริสติก (ฮิวริสติก)

ในความเป็นจริง Fiat-Shamir ฮิวริสติก (ฮิวริสติก) คือการใช้ฟังก์ชันแฮชเพื่อแฮชสคริปต์ที่สร้างไว้ก่อนหน้านี้เพื่อให้ได้ค่าซึ่งใช้เป็นค่าท้าทาย

คำอธิบายภาพ

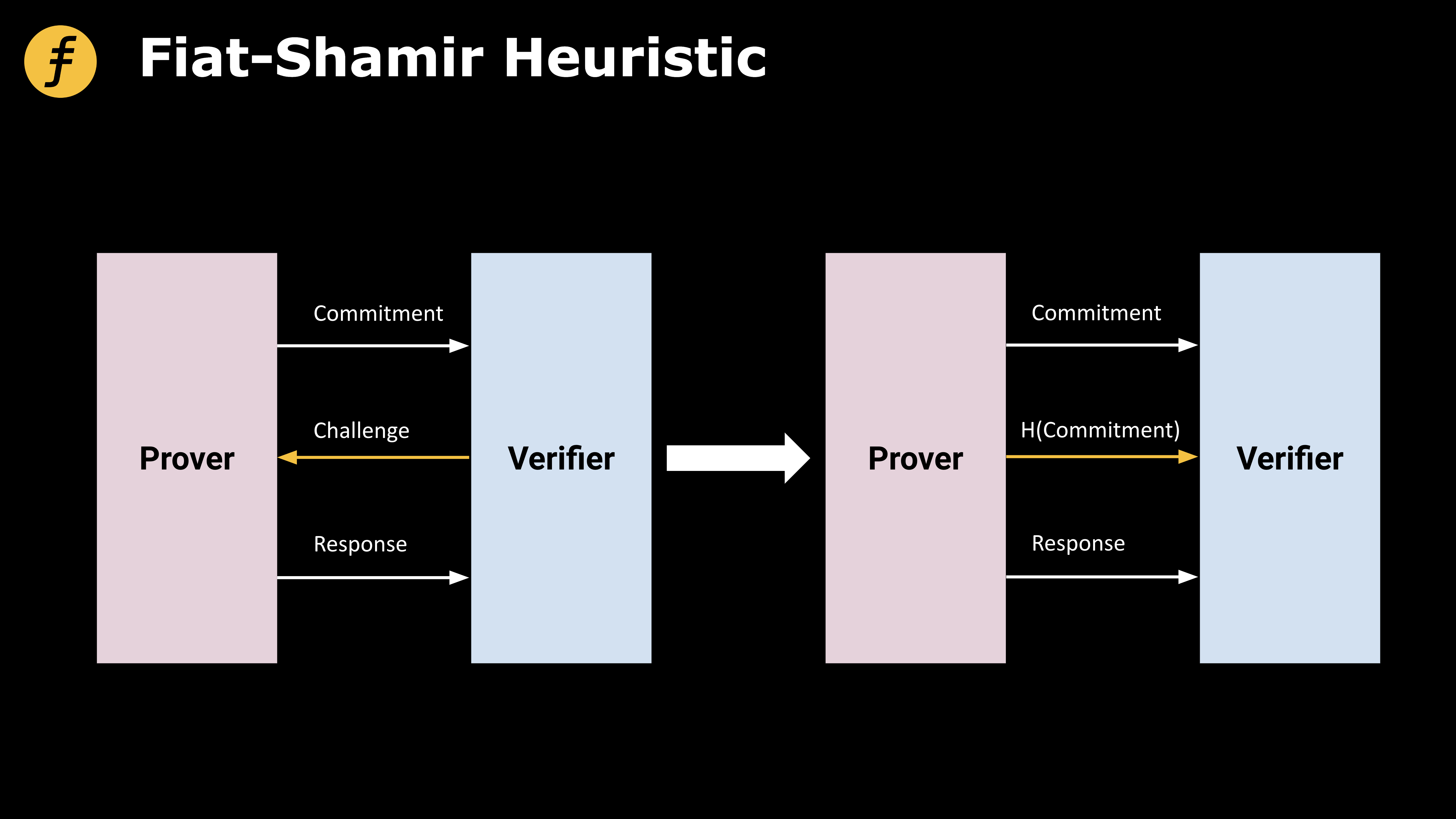
ชื่อระดับแรก

FOAKS ที่ไม่โต้ตอบ

ในส่วนนี้ เราสาธิตการใช้งาน Fiat-Shamir heuristic ในโปรโตคอล FOAKS โดยเฉพาะ ซึ่งส่วนใหญ่ใช้เพื่อสร้างความท้าทายในส่วนเบรกดาวน์ ดังนั้น จึงตระหนักถึง FOAKS ที่ไม่โต้ตอบ

คำอธิบายภาพ

รูปที่ 2: การตรวจสอบเบรกดาวน์ใน FOAKS แบบไม่โต้ตอบ

ตอนนี้เราใช้ฟังก์ชันแฮชและให้ผู้พิสูจน์สร้างเวกเตอร์สุ่มนี้ขึ้นมาเอง

ให้ γ0 =H(C1 , R, r0 , r1 ) ตามลําดับ ในการคำนวณการยืนยันของตัวตรวจสอบ จะต้องเพิ่มขั้นตอนการคำนวณ γ0 นี้ด้วย ตามโครงสร้างนี้ จะพบว่าก่อนที่จะสร้างข้อผูกมัด ผู้พิสูจน์ไม่สามารถคาดการณ์มูลค่าความท้าทายล่วงหน้าได้ ดังนั้นจึงไม่สามารถ "โกง" ตามมูลค่าความท้าทายล่วงหน้าได้ นั่นคือสร้างมูลค่าความมุ่งมั่นที่ผิดพลาดสอดคล้องกัน ในเวลาเดียวกัน ตามแฮช การสุ่มของเอาต์พุตฟังก์ชัน ค่าการท้าทาย ยังเป็นไปตามการสุ่ม

สำหรับจุดที่สอง ให้ Î =H(C1 , R, r0 , r1 , c1 , y1 , cγ 0 , yγ 0 )

บทส่งท้าย

1. function PC. Commit(ϕ)：

2. Parse was a k × k matrix. The prover locally computes the tensor code encoding C1 ，C2  ，C1  is a k × n matrix，C2  is a n × n matrix.

3. for i ∈ [n] do

4. Compute the Merkle tree root Roott=Merkle.Commit(C2 [:, i])

5. Compute a Merkle tree root R=Merkle.Commit([Root0 ,......Rootn-1 ]), and output R as the commitment.

6. function PC. Prover(ϕ, X, R)

7. The prover generates a random vector γ0  ∈ Fk by computing: γ0 =H(C1 , R, r0 , r1 )

8. Proximity:

   

   
   

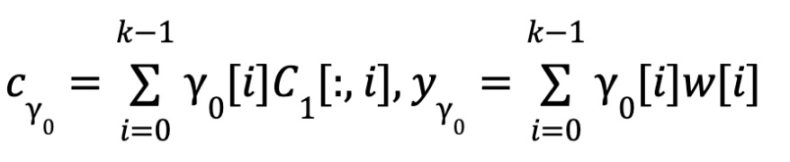
9. Consistency:

   

   
   

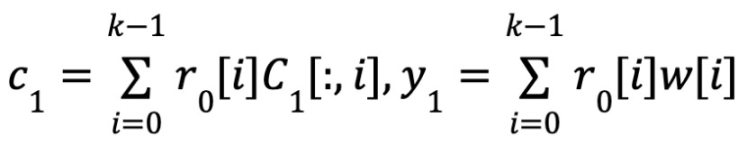
10. Prover sends c1 , y1 , cγ 0 , yγ 0  to the verifier.

11. Prover computes a vector Î as challenge, in which Î = H(C1 , R, r0 , r1 , c1 , y1 , cγ 0 , yγ 0 )

12. for idx ∈ Î do

13. Prover sends C1  [:, idx] and the Merkle tree proof of Rootidx for C2  [:, idx] under R to verifier

14. function PC. VERIFY_EVAL(ΠX, X, y= ϕ (X), R)

15. Proximity: ∀idx ∈ Î, Cγ 0 [idx] == <γ0 , C1 [:, idx]> and Ec(yγ 0 ) == Cγ 0 

16. Consistency: ∀idx ∈ Î, C1  [idx] == <γ0 , C1 [:, idx]> and Ec(y1 ) == C1 

17. y==

18. ∀idx ∈ Î, Ec ( C1 [:, idx]) is consistent with ROOTidx, and ROOTidx’s Merkle tree proof is valid.

19. Output accept if all conditions above holds. Otherwise output reject.

บทส่งท้าย

อ้างอิง

อ้างอิง

1.Fiat, Amos; Shamir, Adi ( 1987). "How To Prove Yourself: Practical Solutions to Identification and Signature Problems". Advances in Cryptology — CRYPTO' 86. Lecture Notes in Computer Science. Springer Berlin Heidelberg. 263: 186 – 194. doi: 10.1007/3-540-47721-7 _ 12. ISBN 978-3-540-18047-0.

2.https://www.cnblogs.com/zhuowangy 2 k/p/12246575.html