สมุดปกขาวการออกแบบ Curve Stablecoin (ฉบับอ้างอิงภาษาจีนและอังกฤษ)
ชื่อระดับแรกCurve Finance
การรวบรวมต้นฉบับ:JamesX，iZUMi Research
Overview
The design of the stablecoin has few concepts: lending-liquidating amm algorithm (LLAMMA), PegKeeper, Monetary Policy are the most important ones. But the main idea is in LLAMMA: replacing liquidations with a special-purpose AMM.
คำอธิบายภาพ
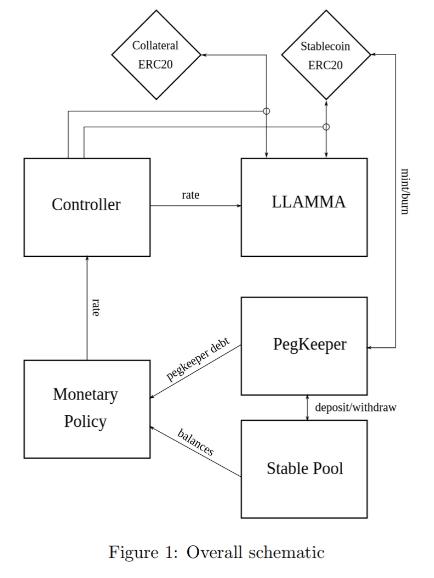
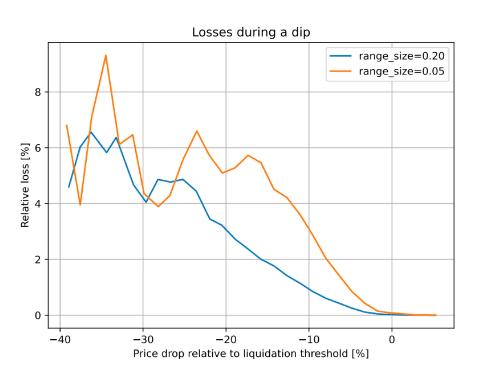
Figure 2 : Dependence of the loss on the price shift relative to the liquidation threshold. Time window for the observation is 3 days
ข้อความ
In this design, if someone borrows against collateral, even at liquidation threshold, and the price of collateral dips and bounces - no significant loss happen. For example, according to simulations using historic data for ETH/USD since Sep 2017 , if one leaves the CDP unattended for 3 days and during this time the price drop of 10% below the liquidation threshold happened - only 1% of collateral gets lost.
ชื่อเรื่องรอง
AMM for continuous liquidation/deliquidation (LLAMMA)
การชำระบัญชีอย่างต่อเนื่อง/AMM โดยไม่มีการชำระบัญชี (LLAMMA)
The core idea of the stablecoin design is Lending-Liquidating AMM Algorithm. The idea is that it converts between collateral (for example, ETH) and the stablecoin (let’s call it USD here). If the price of collateral is high - a user has deposits all in ETH, but as it goes lower, it converts to USD. This is very different from traditional AMM designs where one has USD on top and ETH on the bottom instead.
แนวคิดหลักของการออกแบบ Stablecoin คืออัลกอริทึม AMM ที่ให้ยืม-ชำระบัญชี แนวคิดคือการแปลงระหว่างหลักประกัน (เช่น ETH) และ Stablecoin (ขอเรียกว่า USD) หากราคาของหลักประกันสูง เงินฝากของผู้ใช้ทั้งหมดจะเป็น ETH แต่เมื่อราคาต่ำลง เงินนั้นจะถูกแปลงเป็น USD Stablecoin สิ่งนี้แตกต่างอย่างมากจากการออกแบบ AMM แบบดั้งเดิม การออกแบบ AMM แบบดั้งเดิมคือการวาง USD stablecoin ที่ด้านบน (ครึ่งบนของเส้นโค้ง AMM) และ ETH ที่ด้านล่าง (ครึ่งล่างของเส้นโค้ง AMM)
The below description doesn’t serve as fully self-consistent rigorous proofs. A lot of that (especially the invariant) are obtained from dimensional considerations. More research might be required to have a full mathematical description, however the below is believed to be enough to implement in practice.
คำอธิบายต่อไปนี้ไม่ได้ใช้เป็นหลักฐานที่เข้มงวดและสอดคล้องกันอย่างสมบูรณ์ หลายสิ่งหลายอย่าง (โดยเฉพาะค่าคงที่) ถูกพิจารณาจากมิติต่างๆ เพื่อให้มีคำอธิบายทางคณิตศาสตร์ที่สมบูรณ์ อาจจำเป็นต้องมีการวิจัยเพิ่มเติม อย่างไรก็ตาม คำอธิบายด้านล่างนี้ถือว่าเพียงพอที่จะสนับสนุนการใช้งานในสัญญาอัจฉริยะ
This is only possible with an external price oracle. In a nutshell, if one makes a typical AMM (for example with a bonding curve being a piece of hyperbola) and ramps its “center price” from (for example) down to up, the tokens will adiabatically convert from (for example) USD to ETH while proving liquidity in both ways on the way (Fig. 3 ). It is somewhat similar to avoided crossing (also called Landau-Zener transition) in quantum physics (though only as an idea: mathematical description of the process could be very different). The range where the liquidity is concentrated is called band here, at the constant po band has liquidity from pcd to pcu. We seek for pcd(po) and pcu(po) being functions of po only, functions being more steep than linear and, hence, growing faster than po(Fig. 4 ). In addition, let’s defifine prices p↓and p↑ being prices where p↓(po) = po, and p↑(po) = po, defining ends of bands in adiabatic limit (e.g. p = po).
สิ่งนี้เป็นไปได้ผ่านฟีดราคาจากออราเคิลภายนอกเท่านั้น ในระยะสั้น ถ้าใครใช้ AMM ทั่วไป (เช่น เส้นโค้งพันธะคือชิ้นส่วนของไฮเพอร์โบลา) และวาง"ราคาศูนย์"หากต้องการเปลี่ยนจาก (พูด) ลงเป็นขึ้น โทเค็นจะ "แปลงแบบอะเดียแบติก" จาก (พูด) USD เป็น ETH ในขณะที่ให้สภาพคล่องทั้งสองทางในกระบวนการ (รูปที่ 3) สิ่งนี้ค่อนข้างคล้ายคลึงกับ "การหลีกเลี่ยงการข้าม" (หรือที่เรียกว่าการเปลี่ยนผ่านของ Landau-Zener) ในฟิสิกส์ควอนตัม (แม้ว่าจะเป็นเพียงแนวคิด: คำอธิบายทางคณิตศาสตร์ของกระบวนการอาจแตกต่างกันมาก)
คำอธิบายภาพ
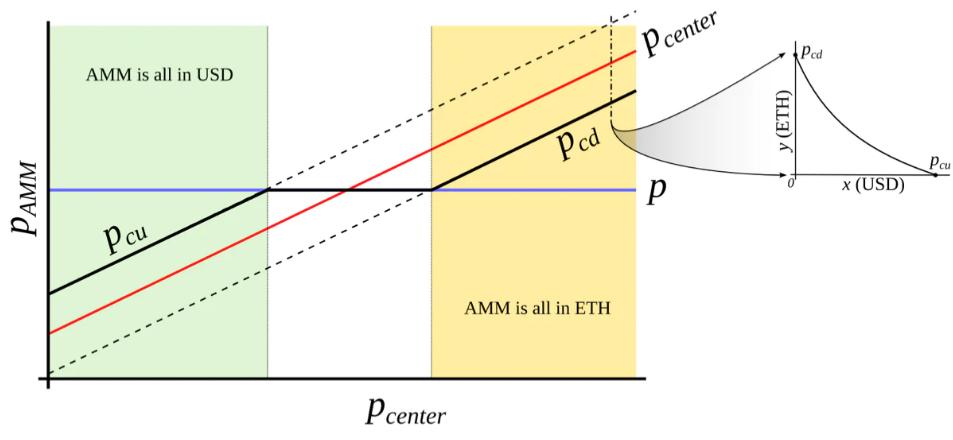Figure 3 : Behavior of an “AMM with an external price source”. External price pcenter determines a price around which liquidity is formed. AMM supports liquidity concentrated from prices pcd to pcu, pcd < pcenter < pcu. When current price p is out of range between pcd and pcu, AMM is either fully in stablecoin (when at pcu) or fully in collateral (when at pcd). When pcd ≤ p ≤ pcu, AMM price is equal to the current price p.
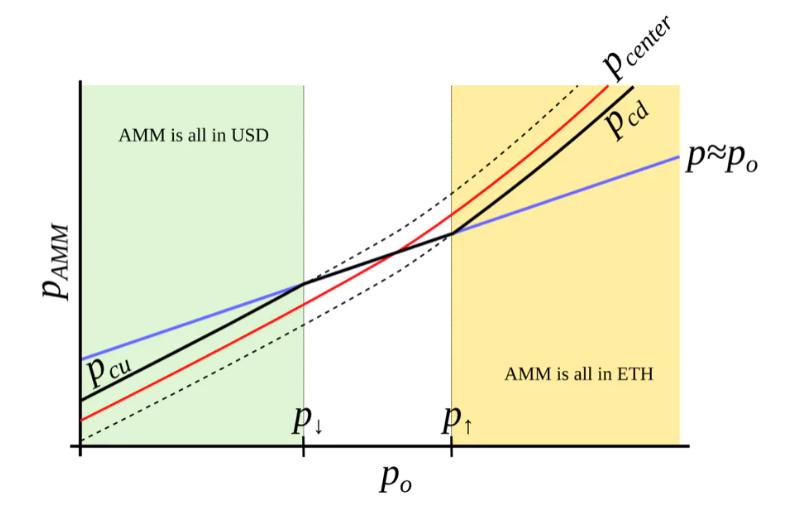Figure 4 : AMM which we search for. We seek to construct an AMM where pcd and pcu are such functions of po that when po grows, they grow even faster. In this case, this AMM will be all in ETH when ETH is expensive, and all in USD when ETH is cheap.
We start from a number of bands where, similarly to Uniswap 3 , hyperbolic shape of the bonding curve is preserved by adding virtual balances. Let say, the amount of USD is x, and the amount of ETH is y, therefore the “amplifified” constant-product invariant would be:
เราเริ่มต้นด้วยแถบบางวง คล้ายกับ Uniswap 3 โดยเพิ่ม "เครื่องชั่งเสมือน" โดยคงรูปร่างไฮเปอร์โบลิกของเส้นโค้งพันธะไว้ สมมติว่าจำนวน USD คือ x และจำนวน ETH คือ y ดังนั้น"ปรับปรุง"ค่าคงที่ - ค่าคงที่ของผลิตภัณฑ์จะเป็น:
We also can denote x 0 ≡ x + f and y 0 ≡ y + g so that the invariant can be written as a familiar I = x 0 y 0. However, f and g do not stay constant: they change with the external price oracle (and so does the invariant I, so it is only the invariant while the oracle price po is unchanged). At a given po, f and g are constant across the band. As mentioned before, we denote p↑ as the top price of the band and p↓as the bottom price of the band. We defifine A (a measure of concentration of liquidity) in such a way that:
เรายังสามารถแสดง x 0 ≡x+f และ y 0 ≡y+g เพื่อให้สามารถเขียนค่าคงที่เป็น I=x 0 y 0 ที่คุ้นเคย อย่างไรก็ตาม f และ g ไม่คงที่: พวกมันเปลี่ยนไปตามการเปลี่ยนแปลงของราคา oracle ภายนอก (เช่นเดียวกับ I ที่ไม่แปรผัน ดังนั้นจึงไม่แปรผันเมื่อราคาของ oracle po คงที่เท่านั้น) ที่ po ที่กำหนด f และ g มีค่าคงที่ตลอดแถบ เช่นเดิม เรากำหนดให้ p↑ เป็นราคาสูงสุดของวงดนตรี และ p↓ เป็นราคาต่ำสุดของวงดนตรี คำจำกัดความของ A (การวัดความเข้มข้นของสภาพคล่อง) มีดังนี้:
The property we are looking for is such that higher price po should lead to even higher price at the same balances, so that the current market price (which will, on average, follow po) is lower than that, and the band will trade towards being all in ETH (and the opposite is also true for the other direction). It is possible to find many ways to satisfy that but we need one:
คุณสมบัติที่เรากำลังมองหาคือ: ราคา po ที่สูงขึ้นควรนำไปสู่ราคาที่สูงขึ้นสำหรับยอดคงเหลือเดียวกัน ดังนั้นราคาตลาดปัจจุบัน (โดยเฉลี่ยจะตาม po) ต่ำกว่าราคานี้และแถบจะเคลื่อนไปสู่ธุรกรรมทั้งหมดใน ทิศทางของ ETH (และทิศทางอื่นๆ ด้วย) มีหลายวิธีที่จะตอบสนองความต้องการ แต่เราต้องการสิ่งนี้:
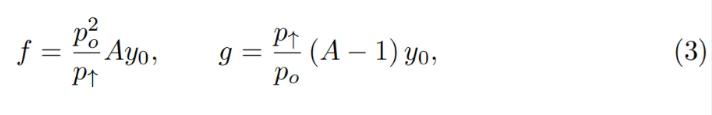
where y 0 is a p 0 -dependent measure of deposits in the current band, denominated in ETH, defifined in such a way that when current price p, p↑ and po are equal to each other, then y = y 0 and x = 0 (see the point at po = p↑ on Fig. 4 ). Then if we substitute y at that moment:
ในหมู่พวกเขา y 0 เป็นตัวบ่งชี้ที่เกี่ยวข้องกับ p 0 เพื่อวัดเงินฝากแบนด์ปัจจุบัน และอยู่ใน ETH คำจำกัดความของมันคือ: เมื่อราคาปัจจุบัน p, p↑ และ po เท่ากัน ดังนั้น y=y 0 , x= 0 (ดูจุดของ po=p↑ ในรูปที่ 4) ดังนั้น ถ้าเราแทนที่ y ในขณะนั้น:
Price is equal to dx 0 /dy 0 which then for a constant-product invariant is:
ราคาเท่ากับ dx 0 /dy 0 ดังนั้นสำหรับผลคูณคงที่ มันคือ:
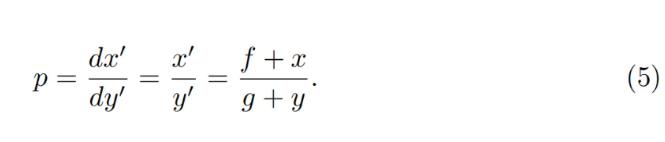
One can substitute situations where po = p↑ or po = p↓ with x = 0 or y = 0 correspndingly to verify that the above formulas are self-consistent.
เราสามารถใช้ x= 0 หรือ y= 0 เพื่อแทนที่ po=p↑ หรือ po=p↓ เพื่อยืนยันว่าสูตรข้างต้นสอดคล้องกัน
Typically for a band, we know p↑ and, hence, p↓, po, constant A, and also x and y (current deposits in the band). To calculate everything, we need to find yo. It can be found by solving the quadratic equation for the invariant:
โดยปกติสำหรับวงดนตรี เรารู้จัก p↑ และดังนั้น p↓, po, ค่าคงที่ A และ x และ y (ค่าสะสมปัจจุบันในวงดนตรี) ในการคำนวณส่วนที่เหลือ เราต้องหาโย่ สามารถพบได้โดยการแก้สมการกำลังสองสำหรับค่าคงที่:
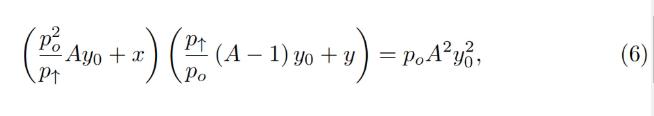
which turns into the quadratic equation against yo:
นี่กลายเป็นสมการกำลังสองสำหรับ yo:
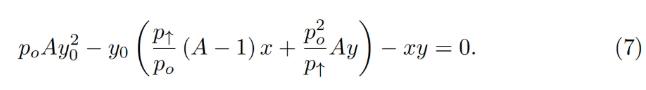
In the smart contract, we solve this quadratic equation in get_y 0 function.
ในสัญญาอัจฉริยะ เราแก้สมการกำลังสองนี้ในฟังก์ชัน get_y 0
While oracle price po stays constant, the AMM works in a normal way, e.g. sells ETH when going up / buys ETH when going down. By simply substituting x = 0 for the “current down” price pcd or y = 0 for the “current up” price pcu values into the equation of the invariant respectively, it is possible to show that AMM prices at the current value of po and the current value of p↑ are:
ด้วยราคาออราเคิลที่คงที่ AMM จะทำงานตามปกติ เช่น ขาย ETH เมื่อราคาสูงขึ้น / ซื้อ ETH เมื่อราคาลดลง เพียงแค่แทนที่ x= 0 ด้วย"ปัจจุบันลดลง"ราคาของ pcd หรือ y= 0 ถูกแทนที่ด้วย"เพิ่มขึ้นในปัจจุบัน"การแทนค่า pcu ของราคา p ลงในสมการที่ไม่แปรผันตามลำดับ สามารถแสดงได้ว่าราคา AMM ภายใต้มูลค่าปัจจุบันของ po และมูลค่าปัจจุบันของ p↑ คือ:
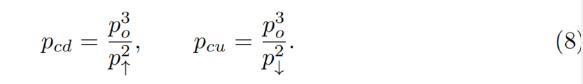
Another practically important question is: if price changes up or down so slowly that the oracle price po is fully capable to follow it adiabatically, what amount y↑ of ETH (if the price goes up) or x↓ of USD (if the price goes down) will the band end up with, given current values x and y and that we start also at p = po. While it’s not an immediately trivial mathematical problem to solve, numeric computations showed a pretty simple answer:
คำถามเชิงปฏิบัติที่สำคัญอีกข้อหนึ่ง: หากราคาเปลี่ยนแปลงช้ามากจนราคาของ oracle สามารถติดตามได้อย่างสมบูรณ์ "แบบอะเดียแบติก" (ภายในแถบ) ให้กำหนดค่าปัจจุบัน x และ y และเราจะเริ่มจากเมื่อ p=po เริ่มต้นเท่าไหร่ y↑ ของ ETH (หากราคาสูงขึ้น) หรือ x↓ ของ USD (หากราคาลดลง) วงนี้จะได้รับ แม้ว่านี่จะไม่ใช่ปัญหาทางคณิตศาสตร์ที่แก้ไขได้ทันที แต่การคำนวณเชิงตัวเลขจะเผยให้เห็นคำตอบที่ค่อนข้างง่าย:
We will use these results when evaluating safety of the loan as well as the potential losses of the AMM.
เราจะใช้ผลลัพธ์เหล่านี้ในการประเมินความปลอดภัยของการให้ยืมและการสูญเสียที่อาจเกิดขึ้นของ AMM
Now we have a description of one band. We split all the price space into bands which touch each other with prices p↓ and p↑ so that if we set a base price pbase and have a band number n:
ตอนนี้เรามีคำอธิบายของวงดนตรี เราแบ่งพื้นที่ราคาทั้งหมดออกเป็นแถบราคาซึ่ง p↓ และ p↑ สัมผัสกัน ดังนั้นหากเรากำหนดราคาพื้นฐาน pbase ด้วยหมายเลขแถบ n:
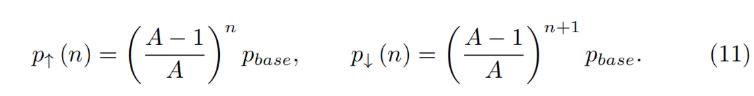
It is possible to prove that the solution of Eq. 7 and Eq. 5 for any band gives:
สำหรับแบนด์ใดๆ แสดงให้เห็นว่าสามารถหาผลเฉลยของสมการที่ 7 และสมการที่ 5 ได้:
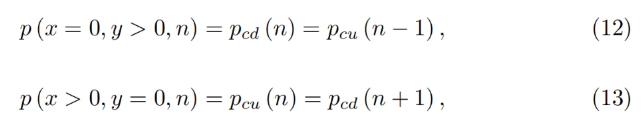
which shows that there are no gaps between the bands.
นี่แสดงให้เห็นว่าไม่มีช่องว่างระหว่างวงดนตรี
Trades occur while preserving the invariant from Eq. 1 , however the current price inside the AMM shifts when the price po: it goes up when po goes down and vice versa cubically, as can be seen from Eq. 8.
ชื่อระดับแรก
LLAMMA vs Stablecoin
Stablecoin is a CDP where one borrows stablecoin against a volatile collateral (cryptocurrency, for example, against ETH). The collateral is loaded into LLAMMA in such a price range (such bands) that if price of collateral goes down relatively slowly, the ETH gets converted into enough stablecoin to cover closing the CDP (which can happen via a self-liquidation, or via an external liquidation if the coverage is too close to dangerous limits, or not close at all while waiting for the price bounce).
Stablecoins เป็น CDP ประเภทหนึ่งที่ผู้คนยืมจากหลักประกันที่ผันผวน (สกุลเงินดิจิทัล เช่น ETH) หลักประกันจะถูกโหลดเข้าสู่ช่วงราคาของ LLAMMA (เช่นแถบ) และหากราคาของหลักประกันตกลงค่อนข้างช้า ETH จะถูกแปลงเป็น Stablecoins ที่เพียงพอเพื่อให้ครอบคลุมการปิด CDP (สิ่งนี้สามารถเกิดขึ้นได้จากการชำระบัญชีด้วยตนเองหรือผ่านการชำระบัญชีภายนอก หาก อัตราจำนองใกล้ถึงขีดอันตรายเกินไปหรือไม่ปิดเลยระหว่างรอราคาดีดกลับ)
When a user deposits collateral and borrows a stablecoin, the LLAMMA smart contract calculates the bands where to locate the collateral. When the price of the collateral changes, it starts getting converted to the stablecoin. When the system is “underwater”, user already has enough USD to cover the loan. The amount of stablecoins which can be obtained can be calculated using a public get_x_down method. If it gives values too close to the liquidation thresholds - an external liquidator can be involved (typically shouldn’t happen within a few days or even weeks after the collateral price went down and sideways, or even will not happen ever if collateral price never goes up or goes back up relatively quickly). A health method returns a ratio of get_x_down to debt plus the value increase in collateral when the price is well above “liquidation”.
เมื่อผู้ใช้ฝากหลักประกันและยืม Stablecoin สัญญาอัจฉริยะ LLAMMA จะคำนวณว่าหลักประกันนั้นอยู่ในวงใด เมื่อราคาของหลักประกันเปลี่ยนแปลง มันจะเริ่มถูกแปลงเป็น Stablecoin เมื่อระบบเข้า"ใต้น้ำ"ผู้ใช้มีเงิน USD เพียงพอที่จะชำระเงินกู้ จำนวนของ Stablecoins ที่สามารถรับสามารถคำนวณได้ด้วยวิธี get_x_down สาธารณะ ถ้ามันให้ค่าที่ใกล้เคียงกับเกณฑ์การชำระบัญชีมากเกินไป ผู้ชำระบัญชีภายนอกสามารถเข้ามาเกี่ยวข้องได้ (ซึ่งโดยปกติแล้วไม่ควรเกิดขึ้นในไม่กี่วันหรือแม้แต่สัปดาห์หลังจากราคาหลักประกันตกลงและไปด้านข้าง แม้ว่าราคาหลักประกันจะไม่เพิ่มขึ้นหรือค่อนข้างเร็วกว่าก็ตาม รถกระบะจะไม่เกิดขึ้น) เมื่อราคาสูงกว่ามาก"เพื่อชำระบัญชี"วิธีที่ดีจะส่งกลับอัตราส่วนของ get_x_down ต่อหนี้ บวกกับมูลค่าหลักประกันที่เพิ่มขึ้น
When a stablecoin charges interest, this should be reflected in the AMM, too. This is done by adjusting all the grid of prices. So, when a stablecoin charges interest rate r, all the grid of prices in the AMM shifts upwards with the same rate r which is done via a base_price multiplier. So, the multiplier goes up over time as long as the charged rate is positive.
เมื่อ Stablecoin คิดดอกเบี้ย สิ่งนี้ควรสะท้อนให้เห็นใน AMM มันต้องสะท้อนด้วย สิ่งนี้ทำได้โดยการปรับกริดทั้งหมดสำหรับราคา ดังนั้นเมื่อ Stablecoin คิดอัตราดอกเบี้ย r ราคาทั้งหมดใน AMM จะขยับขึ้นด้วยอัตราดอกเบี้ยเดียวกัน r และสิ่งนี้ทำได้ผ่านตัวคูณราคาพื้นฐาน ดังนั้น ตราบใดที่อัตราที่เรียกเก็บเป็นบวก ตัวคูณจะเพิ่มขึ้นเมื่อเวลาผ่านไป
When we calculate get_x_down or get_y_up, we are first looking for the amounts of stablecoin and collateral x∗ and y∗ if current price moves to the current price po. Then we look at how much stablecoin or collateral we get if po adiabatically changes to either the lowest price of the lowest band, or the highest price of the highest band respectively. This way, we can get a measure of how much stablecoin we will which is not dependent on the current instantaneous price, which is important for sandwich attack resistance.
เมื่อเราคำนวณ get_x_down หรือ get_y_up สิ่งแรกที่เรามองหาคือจำนวนของ Stablecoin และหลักประกัน x∗ และ y∗ หากราคาปัจจุบันเคลื่อนไปที่ราคาปัจจุบัน จากนั้นเราจะเห็นว่า ถ้า po เปลี่ยนแบบอะเดียแบติกเป็นราคาต่ำสุดในช่วงต่ำสุด หรือราคาสูงสุดในช่วงสูงสุด เราจะได้รับเหรียญ Stablecoins หรือหลักประกันจำนวนเท่าใดตามลำดับ ด้วยวิธีนี้ เราสามารถวัดได้ว่าเราจะได้รับ Stablecoin มากน้อยเพียงใด ซึ่งไม่ขึ้นอยู่กับราคาปัจจุบันในทันที ซึ่งเป็นสิ่งสำคัญสำหรับการต้านทานการโจมตีชั้นลอย **
**
It is important to point out that the LLAMMA uses po defined as ETH/USD price as a price source, and our stablecoin could be traded under the peg (ps < 1 ) or over peg (ps > 1 ). If ps < 1 , then price in the LLAMMA is p > po.
ควรชี้ให้เห็นว่า LLAMMA ใช้ po ที่กำหนดเป็นราคาของ ETH/USD เป็นแหล่งราคา และ Stablecoin ของเราสามารถซื้อขายได้ต่ำกว่า peg (ps<1) หรือสูงกว่า peg (ps>1) ถ้าปล<1 แล้วราคาใน LLAMMA คือ p>po
In adiabatic approximation, p = po/ps, and all the collateral<>stablecoin conversion would happen at a higher oracle price / as if oracle price was lower and equal to:
ในการประมาณแบบอะเดียแบติก p=po/ps หลักประกันทั้งหมด<>การแปลง Stablecoin จะเกิดขึ้นที่ราคา Oracle ที่สูงขึ้น / ราวกับว่าราคา Oracle ต่ำกว่าและเท่ากับ:
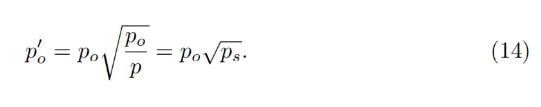
At this price, the amount of stablecoins obtained at conversion is higher by factor of 1/ps (if ps < 1 ) .
ในราคานี้ จำนวนของ Stable Coin ที่ได้รับเมื่อแปลงสกุลเงินจะสูงขึ้น 1 เท่าต่อวินาที (หากเทียบตาม ps<1 ）。
It is less desirable to have ps > 1 for prolonged times, and for that we will use the stabilizer (see next)
ตัวปรับเสถียรภาพอัตโนมัติและนโยบายการเงิน
Automatic Stabilizer and Monetary Policy
ตัวปรับเสถียรภาพอัตโนมัติและนโยบายการเงิน
When ps > 1 (for example, because of the increased demand for stablecoin), there is peg-keeping reserve formed by an asymmetric deposit into a stableswap Curve pool between the stablecoin and a redeemable reference coin or LP token. Once ps > 1 , the PegKeeper contract is allowed to mint uncollateralized stablecoin and (only!) deposit it to the stableswap pool single-sided in such a way that the final price after this is still no less than 1. When ps < 1 , the PegKeeper is allowed to withdraw (asymmetrically) and burn the stablecoin.
เมื่อ ps > 1 (เช่น เนื่องจากความต้องการที่เพิ่มขึ้นสำหรับ stablecoins) จะมีการตรึงสำรองซึ่งเกิดจากการฝากที่ไม่สมมาตรระหว่าง Stablecoins และเหรียญอ้างอิงที่แลกได้หรือโทเค็น LP ไปยังกลุ่ม Curve Pool ของ Stableswap เมื่อ ps>1 สัญญา PegKeeper จะได้รับอนุญาตให้สร้างเหรียญ Stablecoin ที่ไม่มีหลักประกันและฝากไว้ในกลุ่ม Stableswap ด้านเดียวเท่านั้น และราคาสุดท้ายหลังจากทำเช่นนั้นก็ยังไม่ต่ำกว่า 1 เมื่อปล< 1 PegKeeper ได้รับอนุญาตให้ถอน (แบบอสมมาตร) และเผาเหรียญ Stablecoin
These actions cause price ps to quickly depreciate when it’s higher than 1 and appreciate if lower than 1 because asymmetric deposits and withdrawals change the price. Even though the mint is uncollateralized, the stablecoin appears to be implicitly collateralized by liquidity in the stablecoin pool. The whole mint/burn cycle appears, at the end, to be profitable while providing stability.
การกระทำเหล่านี้ทำให้ราคา ps อ่อนค่าอย่างรวดเร็วเหนือ 1 และแข็งค่าต่ำกว่า 1 เนื่องจากการฝากและถอนแบบไม่สมมาตรเปลี่ยนแปลงราคา แม้ว่าส่วนนี้ของ "โรงกษาปณ์" จะไม่มีการค้ำประกัน แต่ Stablecoin ดูเหมือนจะได้รับการสนับสนุนโดยหลักประกันโดยปริยายของสภาพคล่องในกลุ่ม Stablecoin วงจรการผลิตเหรียญกษาปณ์/การเผาไหม้ทั้งหมดดูเหมือนจะให้ผลกำไรในตอนท้าย ในขณะเดียวกันก็ให้ความเสถียร
Let’s denote the amount of stablecoin minted to the stabilizer (debt) as dst and the function which calculates necessary amount of redeemable USD to buy the stablecoin in a stableswap AMM get_dx as fdx(). Then, in order to keep reserves not very large, we use the “slow” mechanism of stabilization via varying the borrow r:
เรามาแสดงจำนวนของ Stablecoins ที่สร้างจาก Stablecoin (หนี้) เป็น dst และฟังก์ชันในการคำนวณจำนวนของ USD ที่แลกได้ซึ่งจำเป็นสำหรับการซื้อ Stablecoin ใน AMM ของ Stableswap get_dx เป็น fdx() จากนั้น เพื่อไม่ให้ "กองหนุน" มีขนาดใหญ่มาก เราจึงใช้"ช้า"กลไกการรักษาเสถียรภาพ
where h is the change in ps at which the rate r changes by factor of 2 (higher ps leads to lower r). The amount of stabilizer debt dst will equilibrate at different value depending on the rate at ps = 1 r 0. Therefore, we can (instead of setting manually) be reducing r 0 while dst/supply is larger than some target number (for example, 5%) (thereby incentivizing borrowers to borrow-and-dump the stablecoin, decreasing its price and forcing the system to burn the dst) or increasing if it’s lower (thereby incentivizing borrowers to return loans and pushing ps up, forcing the system to increase the debt dst and the stabilizer deposits).
ชื่อระดับแรก
สรุป/สรุป
The presented mechanisms can, hopefully, solve the riskiness of liquidations for stablecoin-making and borrowing purposes. In addition, stabilizer and automatic monetary policy mechanisms can help with peg-keeping without the need of keeping overly big PSMs.
หวังเป็นอย่างยิ่งว่ากลไกที่นำเสนอนี้จะจัดการกับความเสี่ยงของการชำระบัญชีเพื่อวัตถุประสงค์ในการทำเหรียญ Stablecoin และการให้ยืม นอกจากนี้ ตัวปรับเสถียรภาพและกลไกนโยบายการเงินอัตโนมัติยังช่วยรักษาจุดยึดราคาไว้โดยไม่จำเป็นต้องรักษา PSM มากเกินไป (โมดูลจุดยึดเสถียรภาพ Peg Stability Module)
