ชื่อเรื่องรอง

1. ความแม่นยำของเลขคณิตทศนิยม

ในปัจจุบัน ภาษาคอมพิวเตอร์กระแสหลักส่วนใหญ่เป็นไปตามมาตรฐาน IEEE 754 สำหรับการแสดงตัวเลขทศนิยม และภาษา Rust ก็ไม่มีข้อยกเว้น ต่อไปนี้คือคำอธิบายของ f64 ชนิดทศนิยมที่มีความแม่นยำสองเท่าในภาษา Rust และรูปแบบการจัดเก็บข้อมูลไบนารีในคอมพิวเตอร์:

รูปภาพ

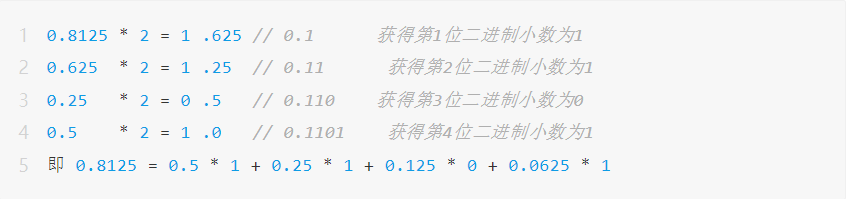
จำนวนจุดลอยตัวจะแสดงในรูปแบบสัญกรณ์วิทยาศาสตร์โดยมีฐานเป็น 2 ตัวอย่างเช่น เลขฐานสอง 0.1101 ที่มีจำนวนหลักจำกัดสามารถใช้แทนทศนิยม 0.8125 ได้ วิธีการแปลงเฉพาะมีดังนี้:

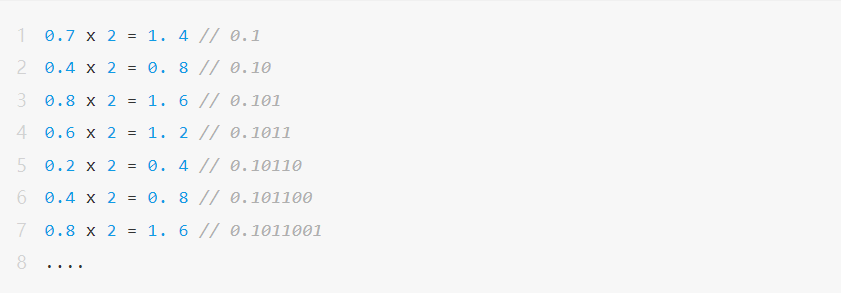
อย่างไรก็ตาม สำหรับทศนิยมอีก 0.7 จะมีปัญหาต่อไปนี้ในกระบวนการแปลงเป็นเลขทศนิยม:

นั่นคือ ทศนิยม 0.7 จะแสดงเป็น 0.101100110011001100.....(infinite loop) ซึ่งไม่สามารถแทนค่าทศนิยมด้วยความยาวบิตจำกัดได้อย่างถูกต้อง และเกิดปรากฏการณ์ "การปัดเศษ (Rounding)" .

สมมติว่าในเครือข่ายสาธารณะ NEAR จำเป็นต้องมีการกระจายโทเค็น NEAR 0.7 รายการไปยังผู้ใช้ 10 คน จำนวนเฉพาะของโทเค็น NEAR ที่แจกจ่ายให้กับผู้ใช้แต่ละรายจะถูกคำนวณและบันทึกไว้ในตัวแปร result_0

ผลลัพธ์ของการดำเนินการกรณีทดสอบนี้เป็นดังนี้:

จะเห็นได้ว่าในการดำเนินการทศนิยมข้างต้น ค่าของจำนวนเงินไม่ได้แสดงถึง 0.7 อย่างถูกต้อง แต่มีค่าใกล้เคียงมากเท่ากับ 0.69999999999999995559 นอกจากนี้ สำหรับการดำเนินการส่วนเดียว เช่น จำนวนเงิน/ตัวหาร ผลการดำเนินงานจะกลายเป็น 0.069999999999999999 ที่ไม่ชัดเจน ไม่ใช่ 0.07 ที่คาดไว้ สิ่งนี้แสดงให้เห็นถึงความไม่แน่นอนของเลขคณิตทศนิยม

1. ในเรื่องนี้ เราจะต้องพิจารณาใช้วิธีการแทนตัวเลขประเภทอื่นในสัญญาอัจฉริยะ เช่น ตัวเลขจุดตายตัว

2. ตามตำแหน่งคงที่ของจุดทศนิยมของจำนวนจุดคงที่ ตัวเลขจุดคงที่มีสองประเภท: จำนวนเต็มจุดคงที่ (บริสุทธิ์) และทศนิยมคงที่ (บริสุทธิ์)

ถ้าจุดทศนิยมคงที่หลังหลักต่ำสุดของตัวเลข จะเรียกว่าจำนวนเต็มจุดคงที่

ในการเขียนสัญญาอัจฉริยะ เศษส่วนที่มีตัวส่วนคงที่มักจะใช้แทนค่าบางอย่าง เช่น เศษส่วน 'x/N' โดยที่ 'N' เป็นค่าคงที่ และ 'x' สามารถเปลี่ยนแปลงได้

ถ้าค่าของ "N" คือ "1,000,000,000,000,000,000" นั่นคือ: ' 10^18 ' ทศนิยมสามารถแสดงเป็นจำนวนเต็มได้ดังนี้:

ใน NEAR Protocol ค่าทั่วไปของ N คือ ' 10^24 ' นั่นคือ 10^24 yoctoNEAR เทียบเท่ากับ 1 โทเค็น NEAR

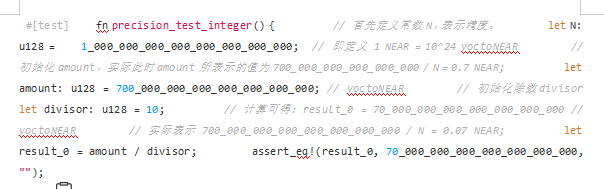
ตามนี้ เราสามารถแก้ไขการทดสอบหน่วยในส่วนนี้เพื่อคำนวณดังนี้:

ด้วยวิธีนี้จะได้ผลลัพธ์การคำนวณตามหลักคณิตศาสตร์ประกันภัย: 0.7 NEAR / 10 = 0.07 NEAR

2. ปัญหาความแม่นยำในการคำนวณจำนวนเต็มสนิม

จากคำอธิบายในส่วนที่ 1 ข้างต้น จะพบว่าการใช้การดำเนินการจำนวนเต็มสามารถแก้ปัญหาการสูญเสียความแม่นยำในการดำเนินการแบบทศนิยมในสถานการณ์การทำงานบางอย่างได้

อย่างไรก็ตาม นี่ไม่ได้หมายความว่าผลลัพธ์ของการคำนวณโดยใช้จำนวนเต็มนั้นถูกต้องและเชื่อถือได้อย่างสมบูรณ์ ส่วนนี้อธิบายสาเหตุบางประการที่ส่งผลต่อความแม่นยำของการคำนวณจำนวนเต็ม

2.1 ใบสั่งงาน

สำหรับการคูณและการหารที่มีลำดับความสำคัญทางเลขคณิตเท่ากัน การเปลี่ยนลำดับอาจส่งผลโดยตรงต่อผลการคำนวณ ทำให้ความแม่นยำในการคำนวณจำนวนเต็มมีปัญหา

ตัวอย่างเช่น มีการดำเนินการดังต่อไปนี้:

ผลลัพธ์ของการดำเนินการทดสอบหน่วยมีดังนี้:

เราพบว่า result_0 = a * c / b และ result_1 = (a / b) * c แม้ว่าสูตรการคำนวณจะเหมือนกัน แต่ผลลัพธ์ต่างกัน

เหตุผลเฉพาะสำหรับการวิเคราะห์คือ: สำหรับการหารจำนวนเต็ม ความแม่นยำที่น้อยกว่าตัวหารจะถูกยกเลิก ดังนั้นในกระบวนการคำนวณ result_1 การคำนวณครั้งแรก (a / b) จะสูญเสียความแม่นยำในการคำนวณก่อนและกลายเป็น 0 ในขณะที่ในการคำนวณ result_0 ผลลัพธ์ของ a * c จะถูกคำนวณก่อน 20_0000 ซึ่งจะมากกว่า กว่าตัวหาร b ดังนั้นจึงหลีกเลี่ยงปัญหาการสูญเสียความแม่นยำและได้ผลการคำนวณที่ถูกต้อง

2.2 ลำดับความสำคัญน้อยเกินไป

ผลลัพธ์เฉพาะของการทดสอบหน่วยนี้มีดังต่อไปนี้:

จะเห็นได้ว่าผลการคำนวณที่เทียบเท่ากันของผลลัพธ์_0 และผลลัพธ์_1 ของกระบวนการคำนวณนั้นไม่เหมือนกัน และผลลัพธ์_1 = 13 นั้นใกล้เคียงกับค่าการคำนวณที่คาดไว้จริง: 13.3333....

3. วิธีเขียนสัญญาสมาร์ทสมาร์ทคณิตศาสตร์ประกันภัยเชิงตัวเลข

การตรวจสอบความแม่นยำที่ถูกต้องเป็นสิ่งสำคัญมากในสัญญาอัจฉริยะ แม้ว่าภาษา Rust ยังมีปัญหาเรื่องการสูญเสียความแม่นยำในผลลัพธ์ของการดำเนินการจำนวนเต็ม เราสามารถใช้มาตรการป้องกันต่อไปนี้เพื่อปรับปรุงความแม่นยำและบรรลุผลลัพธ์ที่น่าพอใจ

• 3.1 ปรับลำดับการทำงานของการดำเนินการ

ชอบการคูณจำนวนเต็มมากกว่าการหารจำนวนเต็ม

3.2 การเพิ่มลำดับขนาดของจำนวนเต็ม

จำนวนเต็มใช้ลำดับความสำคัญที่มากขึ้น สร้างโมเลกุลที่ใหญ่ขึ้น

ตัวอย่างเช่น สำหรับโทเค็น NEAR หากคุณกำหนด N = 10 ตามที่อธิบายไว้ข้างต้น หมายความว่า หากคุณต้องการแสดงค่า NEAR เป็น 5.123 ค่าจำนวนเต็มที่ใช้ในการดำเนินการจริงจะแสดงเป็น 5.123* 10^10 = 51_230_000_000 . ค่านี้ยังคงมีส่วนร่วมในการดำเนินการจำนวนเต็มตามมา ซึ่งสามารถปรับปรุงความแม่นยำของการดำเนินการได้

3.3 การสูญเสียความแม่นยำในการทำงานแบบสะสม

สำหรับปัญหาความแม่นยำในการคำนวณจำนวนเต็มที่ไม่สามารถหลีกเลี่ยงได้ ฝ่ายโครงการสามารถพิจารณาบันทึกการสูญเสียสะสมของความแม่นยำในการคำนวณ

สมมติสถานการณ์การใช้ fn distribution(amount: u128, offset: u128) -> u128 เพื่อแจกจ่ายโทเค็นให้กับผู้ใช้ USER_NUM ดังนี้

ในกรณีทดสอบนี้ ระบบจะแจกจ่าย 10 Token ให้กับผู้ใช้ 3 คนในแต่ละครั้ง อย่างไรก็ตาม เนื่องจากความแม่นยำของการคำนวณจำนวนเต็ม เมื่อคำนวณ per_user_share ในรอบแรก ผลการคำนวณจำนวนเต็มที่ได้รับคือ 10/3 = 3 นั่นคือผู้ใช้ในรอบแรกของการแจกจ่ายจะได้รับ 3 โทเค็นโดยเฉลี่ย และรวมทั้งหมด 9 โทเค็นจะถูกแจกจ่าย

ณ จุดนี้ จะพบว่ายังมีโทเค็นหนึ่งตัวในระบบที่ยังไม่ได้แจกจ่ายให้กับผู้ใช้ ด้วยเหตุผลนี้ จึงถือเป็นการบันทึกโทเค็นที่เหลืออยู่ชั่วคราวในการชดเชยตัวแปรส่วนกลางของระบบ รอครั้งต่อไปที่ระบบเรียกแจกจ่ายเพื่อแจกจ่ายโทเค็นให้กับผู้ใช้ ค่านี้จะถูกนำออกและพยายามแจกจ่ายให้กับผู้ใช้พร้อมกับจำนวนโทเค็นที่แจกจ่ายในรอบนี้

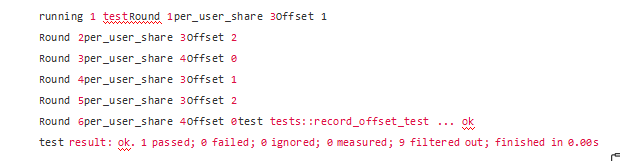
กระบวนการแจกจ่ายโทเค็นจำลองมีดังนี้:

จะเห็นได้ว่าเมื่อระบบเริ่มแจกจ่ายโทเค็นในรอบที่ 3 ค่าชดเชยสะสมของระบบมีถึง 2 และค่านี้จะเพิ่มพร้อมกับโทเค็น 10 โทเค็นที่จะแจกจ่ายในรอบนี้อีกครั้งและแจกจ่ายให้กับผู้ใช้ . (จะไม่มีการสูญเสียความแม่นยำในการคำนวณนี้ per_user_share = token_to_distribute / USER_NUM = 12 / 3 = 4)

โดยรวมแล้วใน 3 รอบแรก ระบบออกโทเค็นทั้งหมด 30 เหรียญ ผู้ใช้แต่ละคนได้รับ 3, 3 และ 4 โทเค็นในแต่ละรอบ ในเวลานี้ ผู้ใช้ยังได้รับโทเค็นทั้งหมด 30 โทเค็น ซึ่งบรรลุเป้าหมายของระบบในการกระจายโบนัสอย่างเต็มที่

3.4 การใช้ห้องสมุด Rust Crate ทศนิยมสนิม

ไลบรารี่ Rust นี้เหมาะสำหรับการคำนวณทางการเงินแบบเศษส่วนที่ต้องการการคำนวณที่แม่นยำและมีประสิทธิภาพและไม่มีข้อผิดพลาดในการปัดเศษ

3.5 พิจารณากลไกการปัดเศษ