ผู้เขียนต้นฉบับ:Vitalik Buterin

ผู้เขียนต้นฉบับ:

• แผนการสุ่มตัวอย่างความพร้อมใช้งานของข้อมูล (DA Sampling หรือ DAS) ปัจจุบันดำเนินการโดยใช้ข้อผูกพันของ KZG ข้อได้เปรียบของสัญญา KZG คือใช้งานง่ายมากและมีคุณสมบัติทางพีชคณิตที่ดีมาก:

• หลักฐานการประเมินมีขนาดคงที่และสามารถตรวจสอบได้ในเวลาคงที่

• ที่นี่มีอัลกอริทึมในการคำนวณการพิสูจน์ทั้งหมดที่ประเมิน deg ที่แต่ละราก N ของเอกภาพในเวลา O(N∗log(N))

• คุณสามารถรวมการผูกมัดเชิงเส้นเพื่อให้ได้การรวมการผูกมัดเชิงเส้น: com(P)+com(Q)=com(P+Q)

คุณสามารถรวมการพิสูจน์เชิงเส้น: Proof(P,x)+Proof(Q,x)+Proof(P+Q,x)

จุดแรกคือการรับประกันประสิทธิภาพที่ดี ประเด็นที่สองทำให้มั่นใจว่าการสร้าง blobs พร้อมสำหรับการสุ่มตัวอย่าง DA นั้นเป็นเรื่องง่าย หากต้องใช้เวลา O(N2) นานขนาดนี้ในการสร้างการพิสูจน์ทั้งหมด ก็จะต้องใช้ตัวดำเนินการที่รวมศูนย์สูงหรืออัลกอริทึมแบบกระจายที่ซับซ้อนเพื่อให้พร้อมสำหรับ DAS

• จุดที่ 3 และ 4 มีค่ามากสำหรับการสุ่มตัวอย่าง 2 มิติ และช่วยให้ผู้ผลิตบล็อกแบบกระจายและรักษาตัวเองได้อย่างมีประสิทธิภาพ:

• ผู้ผลิตบล็อกจำเป็นต้องทราบข้อผูกมัด M ดั้งเดิมเท่านั้นเพื่อใช้ FFT-over-the-curve เพื่อ "ขยายคอลัมน์" และสร้าง

ไม่เพียงแต่คุณทำการสร้างใหม่ต่อแถวได้เท่านั้น แต่คุณยังสามารถสร้างใหม่ต่อคอลัมน์ได้อีกด้วย: ถ้าค่าและการพิสูจน์บางอย่างในคอลัมน์หายไป (แต่ยังมีอยู่มากกว่าครึ่ง) คุณสามารถทำ FFT เพื่อกู้คืน ค่าและหลักฐานที่ขาดหายไปอย่างไรก็ตาม KZG มีจุดอ่อน: อาศัยการเข้ารหัสการจับคู่ที่ซับซ้อนและการตั้งค่าที่เชื่อถือได้ การเข้ารหัสแบบคู่ได้รับการวิจัยและใช้มานานกว่า 20 ปี การตั้งค่าที่เชื่อถือได้คือ 1 สมมติฐานความน่าเชื่อถือใน N โดยที่ N คือผู้เข้าร่วมหลายร้อยคน ดังนั้นความเสี่ยงในทางปฏิบัติจึงสูง และผู้เขียนรู้สึกว่าการใช้ KZG ต่อไปเป็นที่ยอมรับอย่างสมบูรณ์ อย่างไรก็ตาม มันคุ้มค่าที่จะถามคำถาม:

หากเราไม่ต้องการจ่าย KZG เราสามารถใช้ inner product Parameter (IPA) แทนได้หรือไม่

ดูครึ่งแรกของบทความนี้สำหรับคำอธิบายเกี่ยวกับ IPA

• IPA มีคุณสมบัติดังต่อไปนี้:

• การประเมินพิสูจน์ว่ามีขนาดลอการิทึมและสามารถตรวจสอบได้ในเวลาเชิงเส้น (ประมาณ 40 มิลลิวินาทีสำหรับพหุนามขนาด 4096)

• ไม่มีอัลกอริธึมการสร้างหลายหลักฐานที่มีประสิทธิภาพ

• สัญญาผูกมัดเป็นจุดเส้นโค้งวงรี คุณสามารถรวมเข้าด้วยกันเป็นเส้นตรงได้เหมือนสัญญาผูกมัด KZG

ไม่มีวิธีการพิสูจน์ผลรวมเชิงเส้นที่เป็นที่รู้จัก

ดังนั้นเราจึงรักษาคุณสมบัติบางอย่างไว้และสูญเสียบางอย่างไป อันที่จริง เราสูญเสียมามากพอแล้วที่ "วิธีปัจจุบัน" ในการสร้าง แจกจ่าย และพิสูจน์การรักษาด้วยตนเองนั้นไม่สามารถทำได้อีกต่อไป โพสต์นี้อธิบายถึงวิธีการอื่นซึ่งค่อนข้างยุ่งยาก แต่ก็ยังบรรลุเป้าหมาย

ทางเลือก

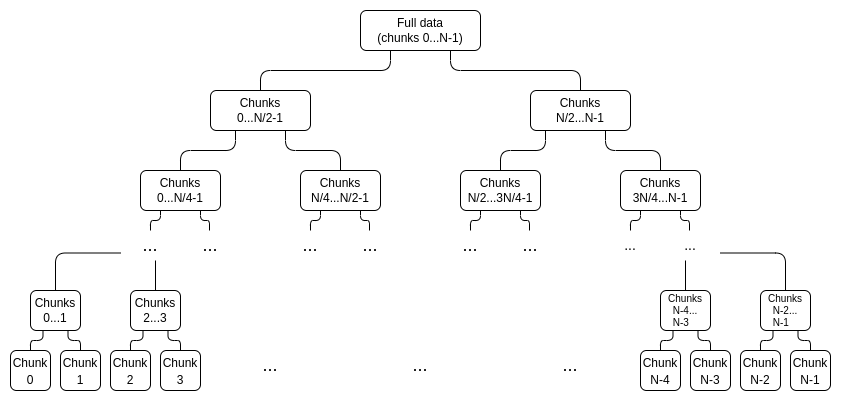
ขั้นแรก เราสร้างแผนผังการพิสูจน์แทนระดับ

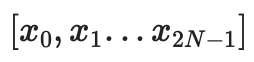
เราตีความข้อมูลในรูปแบบการประเมินโดยถือว่าเป็นเวกเตอร์:

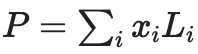
โดยที่พหุนาม

(โดยที่ Li คือ deg<2N พหุนามเท่ากับ 1 ที่พิกัด i และ 0 พิกัดอื่นๆ ในชุด)

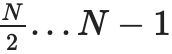
แต่ละโหนดในแผนผังการพิสูจน์คือข้อผูกมัดต่อข้อมูลส่วนนั้น และเป็นการพิสูจน์ว่าข้อผูกมัดนี้ "อยู่ในขอบเขต" จริงๆ ตัวอย่างเช่น,

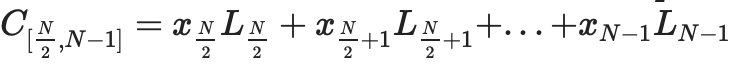
โหนดจะมีสัญญา

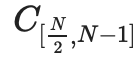
. จะมีใบรับรอง IPA

ที่จริงแล้วเป็นการรวมกันเชิงเส้นของจุดเหล่านี้และไม่มีจุดอื่นๆ

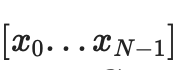
เราสร้างต้นไม้สองต้น ต้นแรกสำหรับ

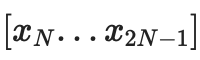
ที่สองสำหรับ
ความมุ่งมั่น "สมบูรณ์" ต่อชิ้นส่วนของข้อมูลประกอบด้วย C[0,N−1] และ C[N,2N−1]

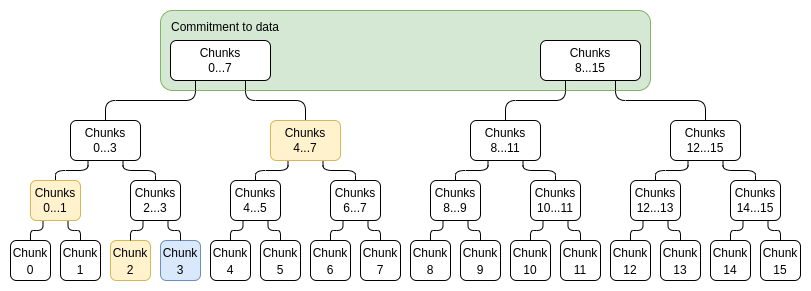
ในการพิสูจน์ค่า xi เฉพาะ เราเพียงจัดเตรียมรายการของคู่ (การยอมจำนน การพิสูจน์) ที่ครอบคลุมช่วงทั้งหมด 0...N−1 หรือ N....2N−1 (แล้วแต่ว่าจะมี i ใดประกอบด้วย) ไม่รวม i และ การกระทำระดับบนสุดที่ฉันไม่ได้เป็นสมาชิกเป็นหลักฐานของการก่อสร้างที่ถูกต้อง ตัวอย่างเช่น ถ้า N=8 และ i=3 การพิสูจน์จะประกอบด้วย C[0,1], C2, C[4,7] และการพิสูจน์ของพวกมัน และการพิสูจน์ว่า C[8,15] ถูกสร้างขึ้นอย่างถูกต้อง หลักฐานจะได้รับการตรวจสอบโดยการตรวจสอบหลักฐานแต่ละรายการและตรวจสอบว่าข้อผูกมัดรวมกันเป็นข้อผูกมัดทั้งหมด

สีน้ำเงิน: ชิ้นที่ 3 สีเหลือง: พิสูจน์ชิ้นที่ 3

โปรดทราบว่าแต่ละอันไม่จำเป็นต้องเป็นการประเมินประสิทธิภาพเพียงครั้งเดียว แต่เราสามารถตัดต้นไม้เพื่อให้อันหนึ่งเป็นชุดของการประเมิน 16 รายการ เนื่องจากขนาดรวมของปรู๊ฟจะใหญ่กว่านี้ อย่างไรก็ตาม เราสูญเสียเพียงเล็กน้อยจากการทำให้ชิ้นใหญ่ขึ้นเช่นนี้

การสร้างหลักฐานเหล่านี้ใช้เวลา O(N∗log(N)) การตรวจสอบการพิสูจน์ใช้เวลา O(N) แต่โปรดทราบว่าการพิสูจน์จำนวนมากสามารถตรวจสอบเป็นชุด: ขั้นตอน O(N) ของการตรวจสอบ IPA คือการผสมเชิงเส้นของเส้นโค้งวงรี ซึ่งหลายขั้นตอนเราสามารถตรวจสอบได้โดยใช้การผสมเชิงเส้นแบบสุ่ม การพิสูจน์แต่ละครั้งยังคงต้องใช้การดำเนินการภาคสนาม O(N) แต่ใช้เวลาเพียง <1 มิลลิวินาทีเท่านั้น

การขยายตัว: fanout (fanout) มากกว่า 2

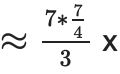
แทนที่จะมี 2 fanout ต่อขั้น เราสามารถมี fanout ที่สูงกว่าได้ เช่น 8 fanouts แทนที่จะมีหลักฐานหนึ่งข้อต่อข้อผูกมัด เราจะมีหลักฐาน 7 ข้อต่อข้อผูกมัด ตัวอย่างเช่น ที่ชั้นล่างสุด เราจะมีหลักฐาน {1,2,3,4,5,6,7}, {0,2,3,4,5,6,7}, {0,1,3 ,4 ,5,6,7} เป็นต้น สิ่งนี้จะเพิ่มงานการสร้างหลักฐานทั้งหมดโดย

(7 การพิสูจน์ต่อโหนด แต่ละขนาดการพิสูจน์คือ 1.75 เท่าของขนาดดั้งเดิม แต่เลเยอร์น้อยลง 3 เท่า ดังนั้นต้องใช้ความพยายามมากขึ้น ~4.08 เท่า) แต่จะลดขนาดการพิสูจน์ลง 3 เท่า

ขนาดหลักฐาน

สมมติว่าเรากำลังจัดการกับ N=128 ชิ้นขนาด 32 (ดังนั้นเราจึงมีพหุนามน้อยกว่า 4096) และการกระจายของ (4x, 4x, 8x) การพิสูจน์สาขาเดียวจะมี 3 IPA ที่มีขนาดรวม 2∗(7+9+12)=56 จุดโค้ง (~1792 ไบต์) บวกกับ 512 ไบต์ของอันนั้น วันนี้ก้อน 256 ไบต์หรือ 512 ไบต์มีหลักฐาน 48 ไบต์

การสร้างการพิสูจน์ต้องใช้การคูณเส้นโค้ง 2∗8192∗(3∗2+7) ทั้งหมด (3*2 สำหรับสอง fanout-4 ชั้น, 7 สำหรับ fanout-8 ชั้น) หรือการคูณทั้งหมด ~212992 ดังนั้นสิ่งนี้จำเป็นต้องทำให้เสร็จอย่างรวดเร็วด้วยคอมพิวเตอร์ที่ทรงพลัง (คอมพิวเตอร์ทั่วไปสามารถคูณได้ในเวลาประมาณ 50 ไมโครวินาที ดังนั้นจะใช้เวลา 10 วินาที ซึ่งนานเกินไปเล็กน้อย) หรือกระบวนการแบบกระจายที่โหนดต่างๆ เชี่ยวชาญในส่วนที่แตกต่างกัน

การตรวจสอบการพิสูจน์ทำได้ง่ายเนื่องจากสามารถพิสูจน์การพิสูจน์เป็นชุดๆ และทำการคูณด้วยเส้นโค้งวงรีเพียงครั้งเดียวเท่านั้น ดังนั้นจึงไม่น่าจะช้าไปกว่าการใช้หลักฐาน KZG

รักษาตัวเอง

ไม่สามารถรักษาตัวเองได้อย่างมีประสิทธิภาพแบบคอลัมน์ต่อคอลัมน์ แต่เราสามารถหลีกเลี่ยงการกำหนดให้มีการแก้ไขเพียงครั้งเดียวเพื่อให้มีข้อมูลทั้งหมด (ชิ้น 2N ทั้งหมดจากพหุนาม 2M ทั้งหมด) ได้หรือไม่

สมมติว่าแถวเดียวหายไปอย่างสมบูรณ์ มันง่ายที่จะใช้คอลัมน์ใดก็ได้เพื่อสร้างค่าใหม่ในแถวที่ขาดหายไปในคอลัมน์นั้น แต่จะพิสูจน์ได้อย่างไร?

เทคนิคที่ง่ายที่สุดคือเศรษฐศาสตร์คริปโต: ทุกคนสามารถออกพันธบัตรโดยอ้างมูลค่าได้ จากนั้นบางคนสามารถใช้การอ้างสิทธิ์นั้นกับหลักฐานสาขาที่พิสูจน์มูลค่าที่แตกต่างกันเพื่อเฉือนผู้ตรวจสอบความถูกต้องนั้น ตราบใดที่มีการอ้างสิทธิ์ที่ถูกต้องตามกฎหมายเพียงพอ บุคคลในเครือข่ายย่อยของธนาคารสามารถรวมการอ้างสิทธิ์และสร้างข้อผูกมัดและหลักฐานใหม่ได้ ผู้ตรวจสอบความถูกต้องอาจจำเป็นต้องออกการอ้างสิทธิ์ดังกล่าวกับดัชนีตัวอย่างที่กำหนดให้กับพวกเขาอีกทางเลือกหนึ่งที่ไม่มีเศรษฐศาสตร์ดิจิทัลแต่ซับซ้อนกว่าและช้ากว่าในทางเทคนิคคือการส่งหลักฐาน M-branch ของมูลค่าตามคอลัมน์นั้น พร้อมด้วยหลักฐานการตรวจสอบความถูกต้อง。