Nguyên văn tác giả: Fox Tech CEO Kang Shuiyue, Fox Tech trưởng khoa học gia Meng Xuanji

Nguyên văn tác giả: Fox Tech CEO Kang Shuiyue, Fox Tech trưởng khoa học gia Meng Xuanji

Với sự lan rộng của các khái niệm như Bitcoin, chuỗi khối và hợp đồng thông minh, ngày càng có nhiều người chú ý đến sự phát triển mạnh mẽ của lĩnh vực Web3. Về mặt công nghệ, nhiều nhà phát triển cũng chú ý đến các giao thức mật mã hỗ trợ chuỗi khối cơ bản. Trong số đó, giao thức chứng minh không kiến ​​thức tỏa sáng với các đặc điểm độc đáo của nó và nó đóng vai trò chính trong việc thực hiện bảo vệ quyền riêng tư và trong dự án zkrollup thực hiện mở rộng hiệu suất Lớp 2.

Bằng chứng không kiến ​​thức là một thuật ngữ chung cho một lớp thuật toán, cho đến nay các nhà nghiên cứu đã phát minh ra nhiều giao thức bao gồm Plonk, Groth 16, zkStark, Virgo, Orion, Foaks, v.v. Các giao thức khác nhau phù hợp với các tình huống tính toán khác nhau, độ phức tạp và hiệu quả cũng khác nhau, ví dụ: Foaks có ưu điểm là thời gian chứng minh tuyến tính và thời lượng chứng minh nhỏ.

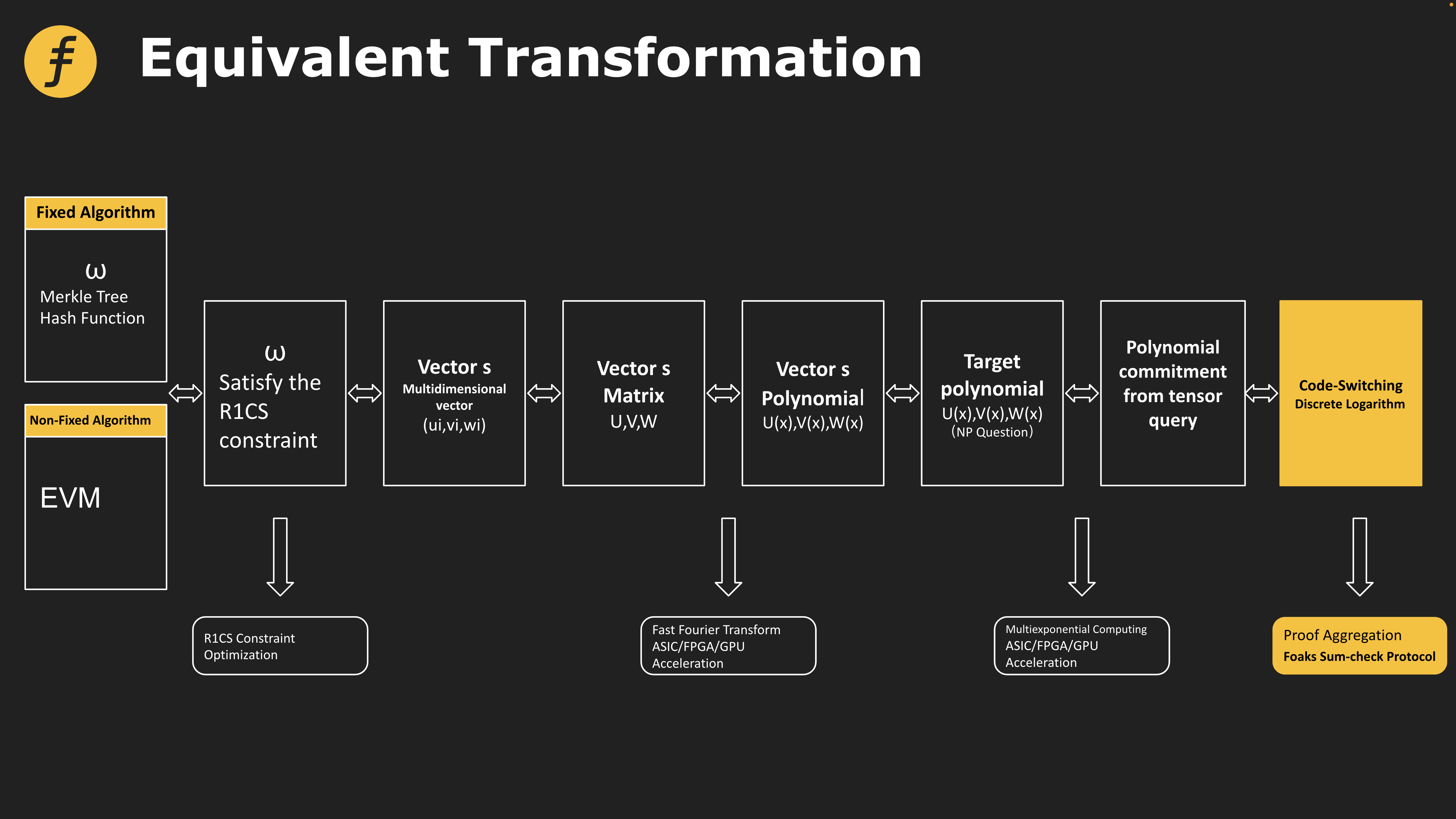
Giao thức này cũng đóng một vai trò quan trọng trong hệ thống bằng chứng Foaks được Fox Tech áp dụng. Cụ thể, để chứng minh tính đúng đắn của opcode, trước tiên cần chuyển đổi nó thành mạch số học, sau đó chuyển đổi thành ma trận, cuối cùng tạo đa thức, áp dụng thuật toán trong hệ thống chứng minh cho đa thức và nén phần chứng minh ở cuối Trong đó, quá trình tương tác giữa người chứng minh (Prover) và người xác minh (Verifier) ​​cũng được chuyển thành quá trình tính một tổng nào đó, tức là quá trình giao thức kiểm tra tổng. .

tiêu đề cấp đầu tiên

Sum-check Protocol

tiêu đề phụ

1. Mục tiêu giao thức

Mục tiêu của giao thức rất đơn giản và dễ hiểu.

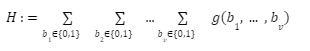
Tương tự như kịch bản “tính toán thuê ngoài” được xem xét trong zkRollup, trong ứng dụng, lượng tính toán của công thức trên sẽ rất lớn, chúng tôi hy vọng sẽ giao việc tính toán công thức này cho người chứng minh (Prover), và sau đó người chứng minh sẽ báo cáo với người kiểm định (Verifier) ​​để chứng minh kết quả tính toán của mình là đúng.

tiêu đề phụ

2. Giả định giao thức

Trước hết, cần làm rõ khả năng của người xác minh trong giao thức này. Chúng tôi giả định rằng người xác minh có một nhà tiên tri (Oracle) có thể tính toán hàm g. Nghĩa là, người xác minh có thể dễ dàng tính toán g(r 1, ... , rv) sau khi xác định một số đầu vào r 1, ... , rv. Nhưng tính toán kết quả đầy đủ H là khó khăn.

Điểm thứ hai, liên quan đến mục tiêu của giao thức, trên thực tế, giao thức kiểm tra tổng có thể tính bBmg(b) cho bất kỳ tập B nào, nhưng không làm mất tính tổng quát, chúng ta giả sử B={0, 1}.

tiêu đề phụ

3. Quy trình giao thức

Thỏa thuận có tổng cộng v vòng. Một biến trong g được xử lý trong mỗi vòng.

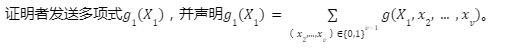
Vòng 1:

Nếu người chứng minh là trung thực, H=g 1( 0)+g 1( 1) nên được thiết lập. Người xác minh sẽ xác minh và nếu vượt qua, số ngẫu nhiên r 1 sẽ được chọn và gửi cho người xác nhận. Lưu ý rằng, theo các giả định của giao thức, người chứng minh có thể hoàn thành việc xác minh trên.

Ta dùng degi(p) để biểu thị bậc của biến thứ i trong đa thức nhiều biến p. Bậc của g 1(X 1) là bậc 1(g), vì vậy chúng ta biết rằng g 1 có thể được biểu diễn bởi bậc 1(g)+ 1 phần tử miền.

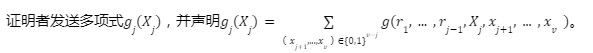
Vòng j (j>1):

vòng v:

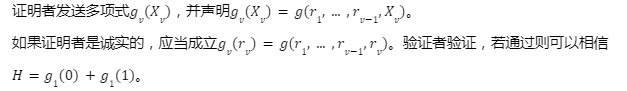
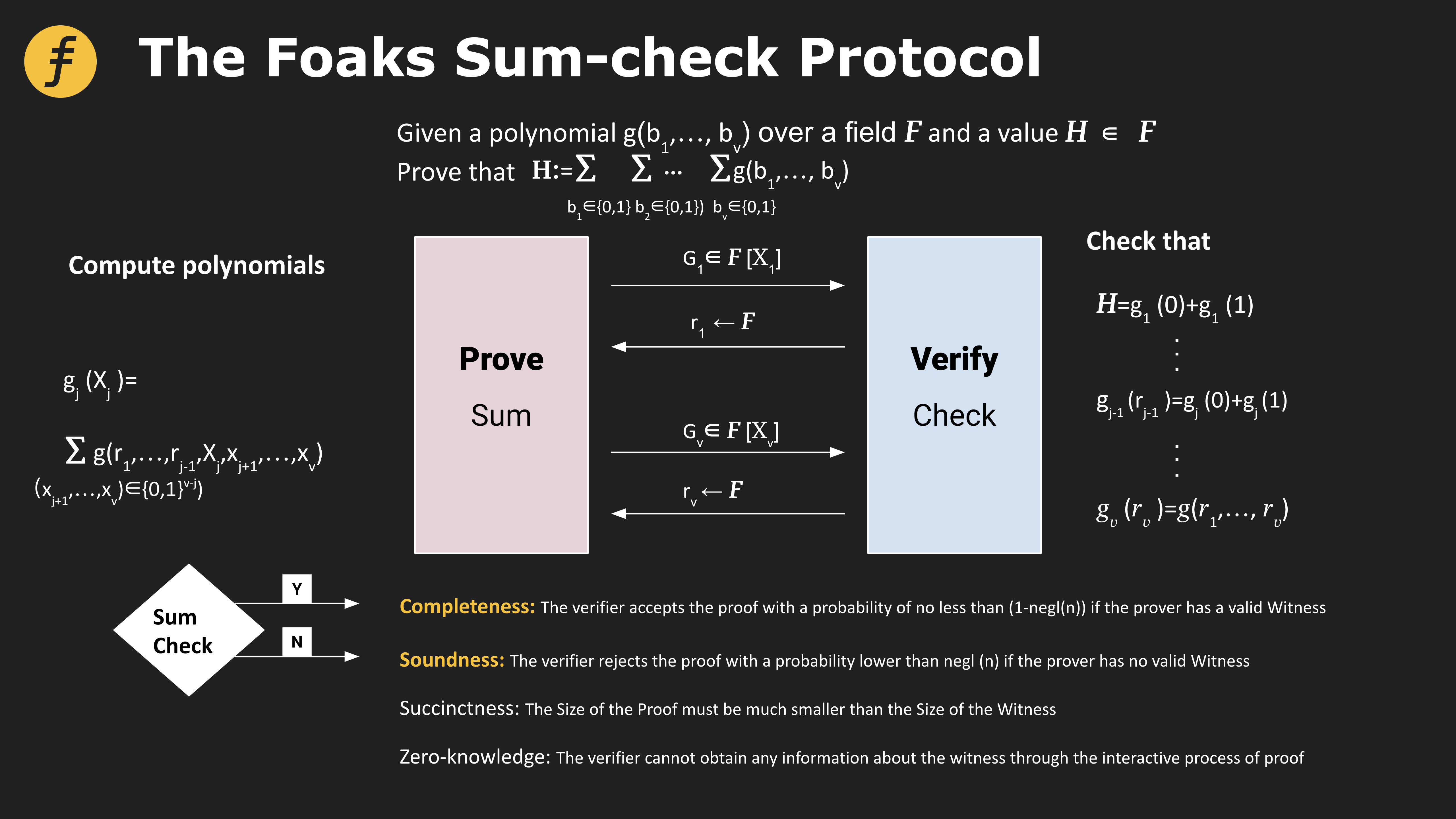
Mô tả hình ảnh

• Hình 2: Giao thức kiểm tra tổng của Foaks

• Tính đầy đủ: Nếu người chứng minh có Nhân chứng hợp lệ, người xác minh sẽ chấp nhận bằng chứng với xác suất không thấp hơn (1-negl(n));

• Tính đúng đắn: Nếu người chứng minh không có Nhân chứng hợp lệ, người xác minh sẽ từ chối bằng chứng với xác suất thấp hơn negl(n)

• Tính ngắn gọn: Quy mô của Bằng chứng phải nhỏ hơn nhiều so với Quy mô của Nhân chứng;

# trong đó negl(n) là bất kỳ chức năng không đáng kể nào

tiêu đề phụ

4. Độ phức tạp của giao thức

Bảng sau đây hiển thị chi tiết các kết quả về độ phức tạp, trong đó T đại diện cho chi phí cần thiết để truy cập một nhà tiên tri (Oracle), nghĩa là để đánh giá g một lần.

Hình 3: Độ phức tạp của giao thức Kiểm tra tổng

tiêu đề cấp đầu tiên

Áp dụng giao thức kiểm tra tổng

Trong số nhiều thuật toán chứng minh không có kiến ​​thức, giao thức kiểm tra tổng đang đóng một vai trò quan trọng. Chứng minh của nhiều vấn đề phụ thuộc vào việc chuyển đổi vấn đề ban đầu thành dạng kiểm tra tổng, sau đó hoàn thành các bước tiếp theo.

Ví dụ, giao thức kiểm tra tổng có thể được sử dụng để đếm số lượng tam giác trong đồ thị vô hướng.

Đầu tiên, chúng ta sử dụng ma trận kề A để biểu diễn đồ thị vô hướng G, gọi E là tập cạnh của nó, khi đó Ai, j= 1(i, j)E, nghĩa là, nếu có một cạnh nằm giữa các điểm i, j thì Ai, j = 1 ngược lại 0. Với các điểm i, j, k thì điều kiện để ba điểm tạo thành một tam giác là Ai, j= 1, Ai, k= 1, Aj, k= 1 .

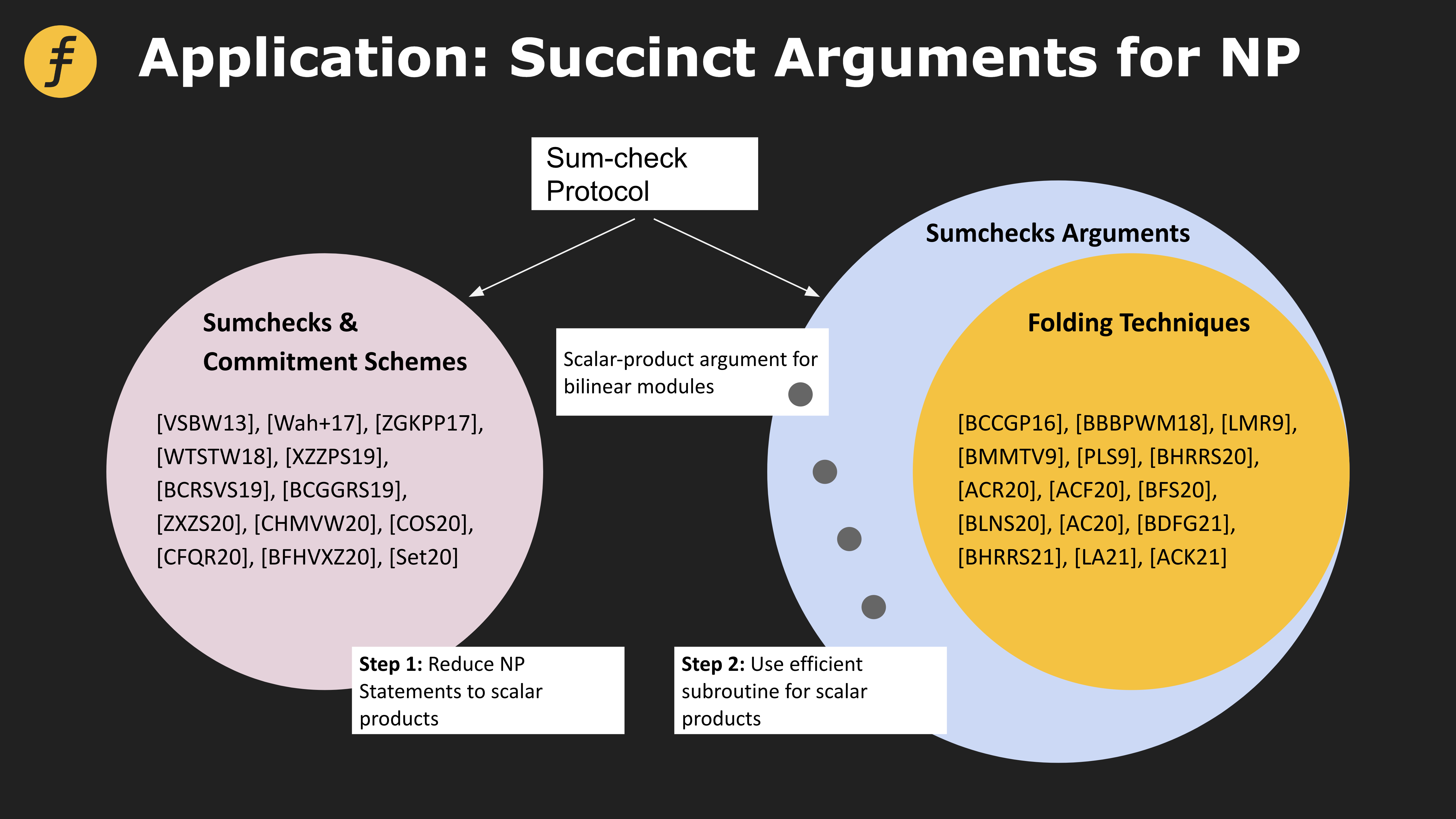
Ngoài ra, trong nhiều hệ thống bằng chứng, giao thức kiểm tra tổng được sử dụng làm logic cơ bản để xây dựng. Hình dưới đây cho thấy các hệ thống bằng chứng khác nhau dựa trên các phép biến đổi khác nhau dựa trên kiểm tra tổng.

Hình 4: Ứng dụng của giao thức Kiểm tra tổng trong bốn loại hệ thống bằng chứng

tiêu đề cấp đầu tiên

phần kết

phần kết

tiêu đề cấp đầu tiên

người giới thiệu

1. [LFKN 92 ] Carsten Lund, Lance Fortnow, Howard Karloff, and Noam Nisan. Algebraic methods for interactive proof systems. J. ACM, 39: 859 – 868, October 1992.

2. https://people.cs.georgetown.edu/jthaler/sumcheck.pdf

3. https://zkproof.org/2020/03/16/sum-checkprotocol/

4. https://eprint.iacr.org/2021/333.pdf

5. người giới thiệuhttps://blog.csdn.net/mutourend/article/details/111610754