เรียนรู้เกี่ยวกับอาร์กิวเมนต์การค้นหาในบทความเดียว

特邀专栏作者

2022-12-22 09:44

บทความนี้มีประมาณ 2848 คำ การอ่านทั้งหมดใช้เวลาประมาณ 5 นาที

บทความนี้จะมุ่งเน้นไปที่อาร์กิวเมนต์ Lookup ซึ่งเป็นหนึ่งในเครื่องมือที่ช่วยให้ OlaVM บรรลุประ

TL;DR

ตามที่กล่าวไว้ในบทความที่แล้ว สวัสดี OlaVM! วิสัยทัศน์ของ OlaVM คือการสร้าง ZKVM ที่มีประสิทธิภาพสูง บทความนี้จะมุ่งเน้นไปที่หนึ่งในเครื่องมือที่ช่วยให้ OlaVM บรรลุประสิทธิภาพที่สูง นั่นคือ Lookup argument อาร์กิวเมนต์การค้นหามีบทบาทสำคัญในการลดขนาดของวงจรเพื่อปรับปรุงประสิทธิภาพของ ZK มีการใช้กันอย่างแพร่หลายในการออกแบบวงจรของ ZKVM จากบทความนี้ คุณสามารถเรียนรู้:

1. Lookup argument จะมีบทบาทอย่างไรใน ZKVM

2. หลักการโปรโตคอล Plookup

3. หลักการโปรโตคอลการโต้แย้งการค้นหาของ Halo 2

ชื่อระดับแรก

The roles in ZKVM

สิ่งที่เรียกว่า ZKVM จริง ๆ แล้วใช้ ZK เพื่อจำกัดกระบวนการดำเนินการทั้งหมดของ VM กระบวนการดำเนินการของ VM โดยทั่วไปสามารถแบ่งออกเป็น: การดำเนินการตามคำสั่ง, การเข้าถึงหน่วยความจำ, การดำเนินการของฟังก์ชันในตัว ฯลฯ ดูเหมือนว่าจะใช้ข้อจำกัดในการดำเนินการเหล่านี้ในการติดตามได้ยากสักหน่อย ประการแรก ข้อจำกัดของประเภทการดำเนินการต่างๆ เพื่อให้สอดคล้องกับความกว้างของการติดตาม ของเสีย จากนั้น หากมีประเภทการดำเนินการที่แตกต่างกันมากเกินไปในการติดตาม จะมีการใช้ Selector มากขึ้น ซึ่งนอกจากจะเพิ่มจำนวนของพหุนามแล้ว ยังเพิ่มลำดับของข้อจำกัดอีกด้วย ในที่สุด เนื่องจาก ขีดจำกัดลำดับของกลุ่ม บรรทัดของการติดตาม จำนวนต้องไม่เกินลำดับของกลุ่มนี้ ดังนั้น ควรลดจำนวนของบรรทัดการติดตามที่ใช้โดยการดำเนินการบางประเภท

ดังนั้น เพื่อความง่าย เราต้องการ:

ก. แบ่งประเภทการดำเนินการต่างๆ ออกเป็นการติดตามย่อยหลายรายการ จากนั้นพิสูจน์แยกกันว่าต้องมีอาร์กิวเมนต์ Lookup ระหว่างการติดตามหลักและการติดตามย่อยเพื่อให้แน่ใจว่าข้อมูลสอดคล้องกัน

ข. สำหรับการคำนวณที่ไม่เป็นมิตรกับ ZK เราสามารถใช้เทคโนโลยีอาร์กิวเมนต์ Lookup เพื่อลดขนาดของการติดตาม เช่น การดำเนินการบิต

ชื่อเรื่องรอง

Lookup between trace tables

คำอธิบายภาพ

รูปที่ 1 ค้นหาระหว่างร่องรอย

ชื่อเรื่องรอง

Lookup for ZK-unfriendly operations

ดังที่ได้กล่าวไว้ก่อนหน้านี้ การพิสูจน์ร่องรอยย่อยแต่ละรายการมีความเป็นอิสระ ดังนั้นการได้รับร่องรอยที่เล็กที่สุดเท่าที่จะเป็นไปได้จะช่วยปรับปรุงประสิทธิภาพของการพิสูจน์ ใช้บิตเป็นตัวอย่าง การดำเนินการในระดับบิตรวมถึง AND, XOR ไม่ใช่สามการดำเนินการ หากคุณต้องการใช้ข้อจำกัดในการทำงานระดับบิตผ่านวงจร สิ่งที่คุณต้องทำคือแยกแต่ละ op ออกเป็นไบนารีลิมบิกหลายตัว หาก ops เหล่านี้กว้าง 3 2 บิต พวกมันจะถูกแบ่งออกเป็น 32 ลิม จากนั้น คุณต้องจำกัด:

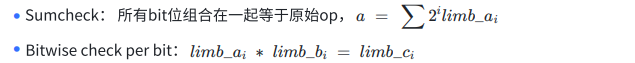
เซลล์การติดตามทั้งหมด 3 + 32 * 3 = 99 เซลล์ถูกครอบครอง และจำนวนข้อจำกัดคือ 3 ผลรวมเช็ค + 32 บิต = 35

คำอธิบายภาพ

รูปที่ 2 การค้นหาในการดำเนินการเลขคณิต

ชื่อระดับแรก

ชื่อเรื่องรอง

ชื่อระดับแรก

ชื่อเรื่องรอง

ชื่อระดับแรก

Extend - 1 : Vector Lookup

Extend - 2 : Multi-tables

Links between Plookup and Lookup

ทั้งโปรโตคอล Plookup และโปรโตคอลการค้นหา Halo 2 สามารถพิสูจน์ได้ว่า f⊂t แต่แนวคิดของโปรโตคอลทั้งสองนั้นแตกต่างกัน และความแตกต่างมีดังนี้:

Plookup จำเป็นต้องใช้ f และ t เพื่อสร้างลำดับใหม่ s องค์ประกอบใน f และ t ปรากฏขึ้นอย่างน้อยหนึ่งครั้งใน s จากนั้นพิสูจน์ว่า s⊂t โดยการเปรียบเทียบชุดระยะทางที่ไม่ใช่ศูนย์ขององค์ประกอบใน s และ t เท่ากัน และสุดท้าย f⊂s⊂t→f⊂t

การค้นหาของ Halo 2 พิสูจน์ f⊂t ได้โดยตรงโดยไม่ต้องสร้างลำดับใหม่ ซึ่งกระชับกว่าการค้นหา

ชื่อระดับแรก