원저자:Vitalik Buterin

원저자:

• 현재 데이터 가용성 샘플링(DA 샘플링 또는 DAS) 체계는 KZG 약정을 사용하여 수행됩니다. KZG Promise의 장점은 사용이 매우 쉽고 몇 가지 훌륭한 대수적 속성을 가지고 있다는 것입니다.

• 평가 증명은 크기가 일정하며 일정한 시간에 검증할 수 있습니다.

• 여기에는 O(N*log(N)) 시간에 N 단위 근 각각에서 deg를 평가하는 모든 증명을 계산하는 알고리즘이 있습니다.

• com(P)+com(Q)=com(P+Q)와 같이 약정을 선형적으로 결합하여 약정의 선형 조합을 얻을 수 있습니다.

증명을 선형으로 결합할 수 있습니다: Proof(P,x)+Proof(Q,x)+Proof(P+Q,x)

첫 번째 요점은 우수한 효율성 보장입니다. 두 번째 요점은 DA 샘플링 준비가 된 blob을 쉽게 생성할 수 있도록 보장합니다. 모든 증명을 생성하는 데 O(N2)가 이렇게 오래 걸리면 DAS 준비를 위해 고도로 중앙 집중화된 액터 또는 복잡한 분산 알고리즘이 필요합니다.

• 세 번째와 네 번째 포인트는 2D 샘플링에 매우 유용하며 분산된 블록 생산자와 효율적인 자가 치유를 가능하게 합니다.

• 블록 생산자는 FFT-over-the-curve를 사용하여 "열을 확장"하고

행 단위 재구성을 수행할 수 있을 뿐만 아니라 열 단위 재구성도 수행할 수 있습니다. 열의 일부 값과 증명이 누락된 경우(그러나 절반 이상이 여전히 사용 가능한 경우) FFT를 수행하여 해당 열을 복구할 수 있습니다. 결 측값 및 증명.그러나 KZG에는 약점이 있습니다. 복잡한 페어링 암호화 및 신뢰할 수 있는 설정에 의존합니다. 쌍 암호화는 20년 넘게 연구되고 사용되었으며, 신뢰할 수 있는 설정은 N에서 1개의 신뢰 가정이며, 여기서 N은 수백 명의 참가자이므로 실제로 위험이 높으며 저자는 KZG를 계속 사용하는 것이 완벽하게 허용된다고 생각합니다. 그러나 다음과 같은 질문을 할 가치가 있습니다.

KZG 비용을 지불하고 싶지 않다면 대신 IPA(내적 매개변수)를 사용할 수 있습니까?

IPA에 대한 설명은 이 기사의 전반부를 참조하십시오.

• IPA에는 다음과 같은 속성이 있습니다.

• 평가는 대수 크기를 가지며 선형 시간(크기 4096의 다항식에 대해 약 40ms)에서 확인할 수 있습니다.

• 알려진 효율적인 다중 증명 생성 알고리즘은 없습니다.

• 약정은 타원 곡선 포인트이며 KZG 약정과 같이 선형으로 결합할 수 있습니다.

선형 조합 증명에 대해 알려진 방법은 없습니다.

따라서 일부 속성은 유지하고 일부는 잃습니다. 사실, 우리는 증거를 생성, 배포 및 자가 치유하는 "현재 방법"이 더 이상 가능하지 않을 만큼 충분히 잃었습니다. 이 게시물은 약간 투박하지만 여전히 목표를 달성하는 대체 방법을 설명합니다.

대안

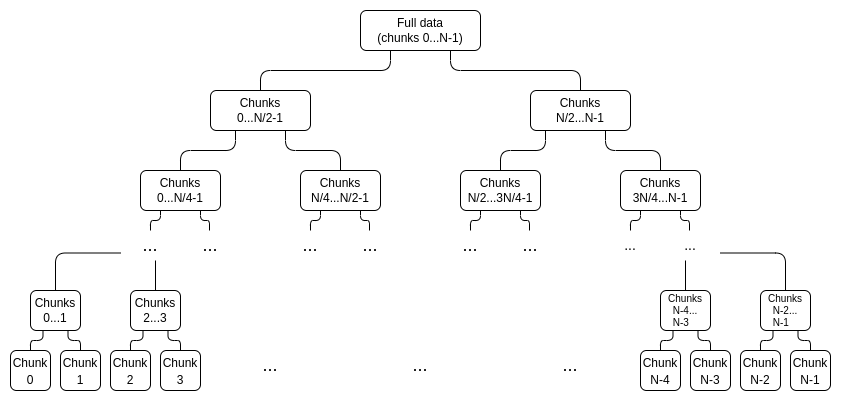
먼저 deg 대신 증명 트리를 생성합니다.

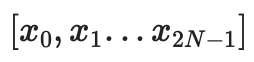
데이터를 벡터로 취급하여 평가 형식으로 해석합니다.

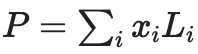
, 여기서 다항식

(여기서 Li는 좌표 i에서 1이고 세트의 다른 좌표에서 0인 deg<2N 다항식입니다).

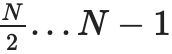
증명 트리의 각 노드는 데이터의 해당 부분에 대한 커밋이며 이 커밋이 실제로 "한계 내"라는 증명입니다. 예를 들어,

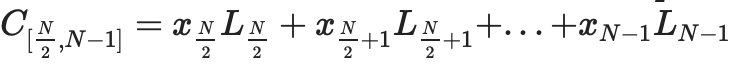
노드는 약속을 포함합니다

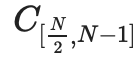
. IPA 인증서가 있을 것입니다.

실제로 이러한 점과 다른 점이 없는 선형 조합입니다.

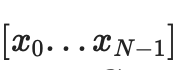
두 개의 트리를 생성합니다.

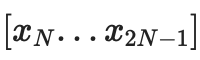
, 두 번째
, 데이터 조각에 대한 "완전한" 커밋은 C[0,N-1] 및 C[N,2N-1]로 구성됩니다.

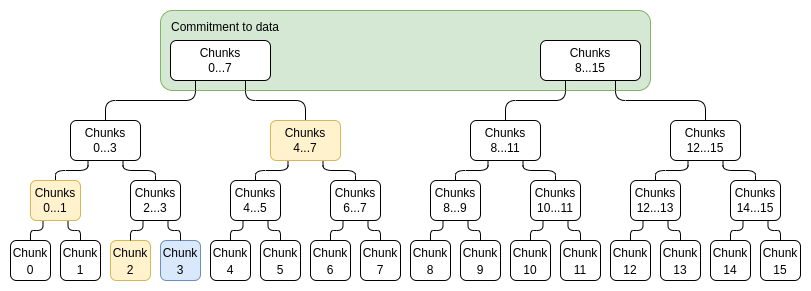
특정 값 xi를 증명하기 위해 전체 범위 0...N−1 또는 N....2N−1(둘 중 i를 포함하는 것), i를 포함하지 않는 전체 범위를 포함하는 (하위 커밋, 증명) 쌍 목록을 제공합니다. 내가 속하지 않은 최상위 커밋은 올바른 구성의 증거입니다. 예를 들어 N=8이고 i=3이면 증명에는 C[0,1], C2, C[4,7] 및 해당 증명과 C[8,15]가 올바르게 구성되었다는 증명이 포함됩니다. 개별 증명을 확인하고 약정이 전체 약정에 합산되는지 확인하여 증명이 확인됩니다.

파란색: 청크 3, 노란색: 청크 3의 증명.

효율성을 위해 각 청크가 단일 평가일 필요는 없으며 대신 청크가 16개의 평가 집합이 되도록 트리를 정리할 수 있습니다. 어쨌든 증명의 결합된 크기가 이것보다 더 클 것이라는 점을 감안할 때, 우리는 이와 같이 청크를 더 크게 만들어서 손실이 거의 없습니다.

이러한 증명을 생성하는 데 O(N*log(N)) 시간이 걸립니다. 증명을 확인하는 데는 O(N) 시간이 걸리지만 많은 증명을 일괄적으로 확인할 수 있습니다. IPA를 확인하는 O(N) 단계는 타원 곡선의 선형 조합이며 그 중 다수는 임의의 선형 조합을 사용하여 확인할 수 있습니다. 각 증명에는 여전히 O(N) 필드 작업이 필요하지만 소요 시간은 1ms 미만입니다.

확장: 팬아웃(fanout)이 2보다 큽니다.

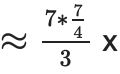
단계당 2개의 팬아웃을 갖는 대신 더 높은 팬아웃(예: 8개의 팬아웃)을 가질 수 있습니다. 약속당 하나의 증명 대신 약속당 7개의 증명이 있습니다. 예를 들어, 맨 아래 레이어에는 증명 {1,2,3,4,5,6,7}, {0,2,3,4,5,6,7}, {0,1,3이 있습니다. ,4 ,5,6,7} 등 이렇게 하면 전체 증명 생성 작업이 다음과 같이 증가합니다.

(노드당 7개의 증명, 각 증명 크기는 원래 크기의 1.75배이지만 레이어가 3배 적기 때문에 ~4.08배의 노력이 더 필요함) 그러나 증명 크기는 3배로 줄어듭니다.

증명 크기

크기가 32인 N=128 청크(따라서 deg<4096 다항식이 있음)와 (4x, 4x, 8x)의 팬아웃을 처리한다고 가정합니다. 단일 분기 증명에는 총 크기가 2*(7+9+12)=56 커브 포인트(~1792바이트)에 청크의 512바이트를 더한 3개의 IPA가 포함됩니다. 오늘날 256바이트 또는 512바이트 청크에는 48바이트 증명이 있습니다.

증명을 생성하려면 총 2*8192*(3*2+7) 곡선 곱셈(두 개의 팬아웃-4 레이어의 경우 3*2, 팬아웃-8 레이어의 경우 7) 또는 총 ~212992 곱셈이 필요합니다. 따라서 이 작업은 강력한 컴퓨터(일반 컴퓨터는 약 50마이크로초 내에 곱셈을 수행할 수 있으므로 10초가 걸리므로 너무 깁니다) 또는 다른 노드가 다른 청크를 전문으로 하는 분산 프로세스에 의해 신속하게 수행되어야 합니다.

증명을 배치로 검증할 수 있고 타원 곡선 곱셈이 한 번만 수행되기 때문에 증명 검증이 쉽습니다. 따라서 KZG 증명을 사용하는 것보다 훨씬 느려서는 안 됩니다.

자가 치유

열 단위로 효과적으로 자가 치유할 수 없습니다. 그러나 모든 데이터(모든 2M 다항식의 모든 2N 청크)를 포함하기 위해 단일 수정이 필요하지 않을 수 있습니까?

단일 행이 완전히 손실되었다고 가정합니다. 해당 열에서 누락된 행의 값을 재구성하기 위해 임의의 열을 사용하는 것은 쉽습니다. 그러나 그것을 어떻게 증명할 것인가?

가장 간단한 기술은 암호화 경제학입니다. 누구나 단순히 가치를 주장하는 채권을 발행할 수 있고, 누군가는 그 주장을 다른 가치를 증명하는 분기 증명과 함께 사용하여 해당 유효성 검사기를 삭감할 수 있습니다. 정당한 청구가 충분히 가능하다면 은행 서브넷의 누군가가 청구를 종합하고 약정과 증거를 재구성할 수 있습니다. 유효성 검사기는 자신에게 할당된 샘플 인덱스에 대해 이러한 클레임을 발행해야 할 수도 있습니다.암호경제학은 없지만 기술적으로 더 복잡하고 느린 대안은 올바른 검증 증명과 함께 해당 열을 따라 값의 M-브랜치 증명을 전달하는 것입니다.。