Curve Stablecoin 設計ホワイトペーパー (中国語および英語の参考版)

最初のレベルのタイトルCurve Finance

オリジナルの編集:JamesX，iZUMi Research

Overview

The design of the stablecoin has few concepts: lending-liquidating amm algorithm (LLAMMA), PegKeeper, Monetary Policy are the most important ones. But the main idea is in LLAMMA: replacing liquidations with a special-purpose AMM.

画像の説明

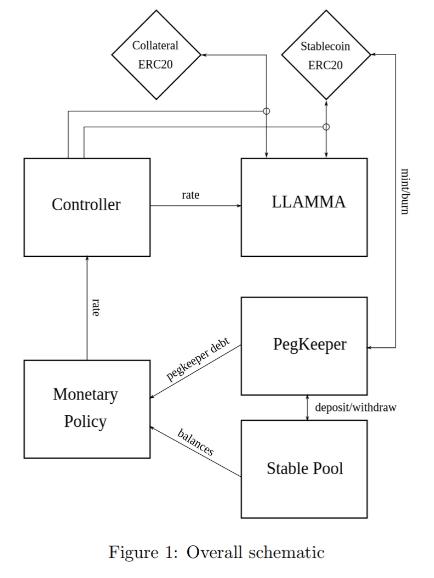
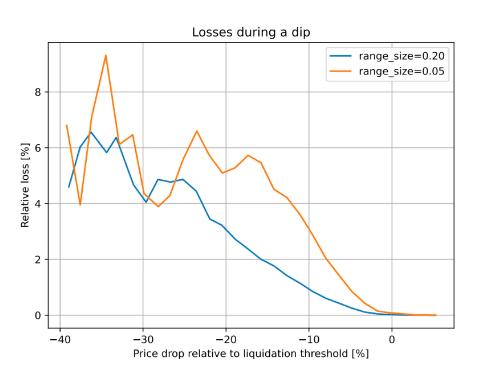
Figure 2 : Dependence of the loss on the price shift relative to the liquidation threshold. Time window for the observation is 3 days

文章

In this design, if someone borrows against collateral, even at liquidation threshold, and the price of collateral dips and bounces - no significant loss happen. For example, according to simulations using historic data for ETH/USD since Sep 2017 , if one leaves the CDP unattended for 3 days and during this time the price drop of 10% below the liquidation threshold happened - only 1% of collateral gets lost.

副題

AMM for continuous liquidation/deliquidation (LLAMMA)

継続的清算/清算を伴わないAMM (LLAMMA)

The core idea of the stablecoin design is Lending-Liquidating AMM Algorithm. The idea is that it converts between collateral (for example, ETH) and the stablecoin (let’s call it USD here). If the price of collateral is high - a user has deposits all in ETH, but as it goes lower, it converts to USD. This is very different from traditional AMM designs where one has USD on top and ETH on the bottom instead.

ステーブルコイン設計の核となるアイデアは、貸付-清算AMMアルゴリズムです。そのアイデアは、担保 (ETH など) とステーブルコイン (ここでは USD と呼びましょう) の間で変換するということです。担保の価格が高い場合、ユーザーのデポジットはすべて ETH ですが、価格が低い場合は USD のステーブルコインに変換されます。これは従来の AMM 設計とは大きく異なり、従来の AMM 設計は、USD ステーブルコインを上部 (AMM 曲線の上半分) に配置し、ETH を下部 (AMM 曲線の下半分) に配置することです。

The below description doesn’t serve as fully self-consistent rigorous proofs. A lot of that (especially the invariant) are obtained from dimensional considerations. More research might be required to have a full mathematical description, however the below is believed to be enough to implement in practice.

以下の説明は、完全に自己矛盾のない厳密な証明として機能するものではありません。多くのこと (特に不変条件) はさまざまな次元から考慮されます。完全な数学的説明を得るには、さらに研究が必要になる可能性がありますが、以下の説明はスマート コントラクトの実装をサポートするのに十分であると考えられます。

This is only possible with an external price oracle. In a nutshell, if one makes a typical AMM (for example with a bonding curve being a piece of hyperbola) and ramps its “center price” from (for example) down to up, the tokens will adiabatically convert from (for example) USD to ETH while proving liquidity in both ways on the way (Fig. 3 ). It is somewhat similar to avoided crossing (also called Landau-Zener transition) in quantum physics (though only as an idea: mathematical description of the process could be very different). The range where the liquidity is concentrated is called band here, at the constant po band has liquidity from pcd to pcu. We seek for pcd(po) and pcu(po) being functions of po only, functions being more steep than linear and, hence, growing faster than po(Fig. 4 ). In addition, let’s defifine prices p↓and p↑ being prices where p↓(po) = po, and p↑(po) = po, defining ends of bands in adiabatic limit (e.g. p = po).

これは、外部オラクルからの価格フィードを通じてのみ可能です。簡単に言うと、典型的な AMM (たとえば、結合曲線は双曲線の一部) を使用すると、次のようになります。"中心価格"(たとえば) ダウンからアップに移行するには、トークンは (たとえば) USD から ETH に「断熱的に」変換され、そのプロセスで双方向の流動性が提供されます (図 3)。これは、量子物理学における「交差の回避」（ランダウ・ツェナー転移としても知られる）に多少似ています（ただし、単なる概念です。プロセスの数学的記述は大きく異なる場合があります）。

画像の説明

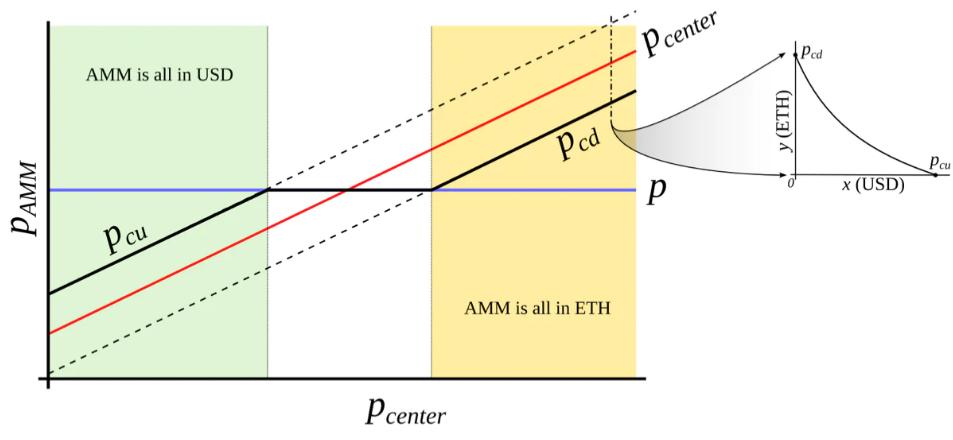Figure 3 : Behavior of an “AMM with an external price source”. External price pcenter determines a price around which liquidity is formed. AMM supports liquidity concentrated from prices pcd to pcu, pcd < pcenter < pcu. When current price p is out of range between pcd and pcu, AMM is either fully in stablecoin (when at pcu) or fully in collateral (when at pcd). When pcd ≤ p ≤ pcu, AMM price is equal to the current price p.

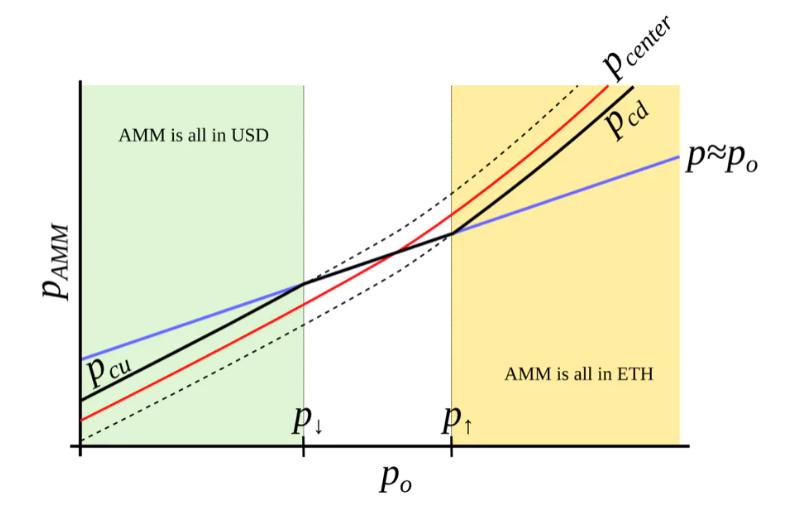Figure 4 : AMM which we search for. We seek to construct an AMM where pcd and pcu are such functions of po that when po grows, they grow even faster. In this case, this AMM will be all in ETH when ETH is expensive, and all in USD when ETH is cheap.

We start from a number of bands where, similarly to Uniswap 3 , hyperbolic shape of the bonding curve is preserved by adding virtual balances. Let say, the amount of USD is x, and the amount of ETH is y, therefore the “amplifified” constant-product invariant would be:

Uniswap 3 と同様に、結合曲線の双曲線形状を維持しながら「仮想バランス」を追加することで、いくつかのバンドから始めます。 USD の量が x で、ETH の量が y であるとします。"強化された"定数 - 積の不変条件は次のようになります。

We also can denote x 0 ≡ x  +  f and y 0 ≡ y + g so that the invariant can be written as a familiar I =  x 0 y 0. However, f and g do not stay constant: they change with the external price oracle (and so does the invariant I, so it is only the invariant while the oracle price po is unchanged). At a given po, f and g are constant across the band. As mentioned before, we denote p↑ as the top price of the band and p↓as the bottom price of the band. We defifine A (a measure of concentration of liquidity) in such a way that:

x 0 ≡x+f および y 0 ≡y+g も表すことができるため、不変式はよく知られた I=x 0 y 0 として書くことができます。ただし、f と g は一定ではありません。外部のオラクル価格が変化すると変化します (不変量 I も同様なので、オラクル価格 po が一定の場合にのみ不変です)。特定の po では、f と g は帯域全体で一定です。前と同様に、p↑ をバンドの最高価格、p↓ をバンドの最低価格として表します。 A (流動性集中の尺度) の定義は次のとおりです。

The property we are looking for is such that higher price po should lead to even higher price at the same balances, so that the current market price (which will, on average, follow po) is lower than that, and the band will trade towards being all in ETH (and the opposite is also true for the other direction). It is possible to find many ways to satisfy that but we need one:

私たちが探している特性は次のとおりです。PO 価格が高くなると、同じ残高の価格も高くなるはずです。そのため、現在の市場価格 (平均して、PO に従う) はこの価格を下回り、バンドはすべての取引に向けて移動します。 ETH の方向 (および他の方向も同様)。満足させる方法はたくさんありますが、必要なのは次の方法です。

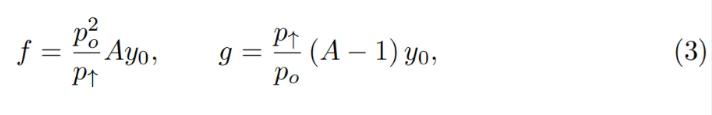
where y 0 is a p 0 -dependent measure of deposits in the current band, denominated in ETH, defifined in such a way that when current price p, p↑ and po are equal to each other, then y = y 0 and x = 0 (see the point at po = p↑ on Fig. 4 ). Then if we substitute y at that moment:

このうち、y 0 はETHにおける現在のバンドデポジットを計測するためのp 0 に関連する指標であり、その定義は、現在の価格p、p↑、poが等しいとき、y=y 0 となります。 、x= 0 (図 4 の po=p↑ の点を参照)。したがって、その時点で y を置き換えると次のようになります。

Price is equal to dx 0 /dy 0 which then for a constant-product invariant is:

価格が dx 0 /dy 0 に等しい場合、定積不変式の場合、次のようになります。

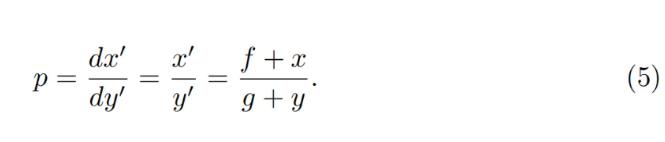
One can substitute situations where po = p↑ or po = p↓ with x = 0 or y = 0 correspndingly to verify that the above formulas are self-consistent.

x= 0 または y= 0 を使用して po=p↑ または po=p↓ を置き換えると、上記の式が自己矛盾がないことを確認できます。

Typically for a band, we know p↑ and, hence, p↓, po, constant A, and also x and y (current deposits in the band). To calculate everything, we need to find yo. It can be found by solving the quadratic equation for the invariant:

通常、バンドについては、p↑、したがって p↓、po、定数 A、そして x と y (バンド内の現在の堆積物) がわかります。残りを計算するには、yo を見つける必要があります。これは、不変量の二次方程式を解くことで求めることができます。

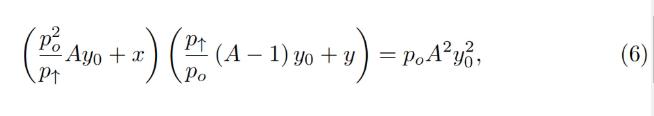
which turns into the quadratic equation against yo:

これは yo の二次方程式になります。

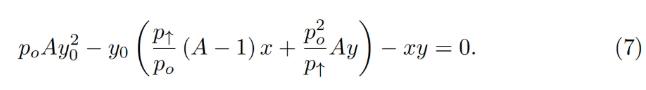
In the smart contract, we solve this quadratic equation in get_y 0 function.

スマート コントラクトでは、get_y 0 関数でこの二次方程式を解きます。

While oracle price po stays constant, the AMM works in a normal way, e.g. sells ETH when going up / buys ETH when going down. By simply substituting x = 0 for the “current down” price pcd or y = 0 for the “current up” price pcu values into the equation of the invariant respectively, it is possible to show that AMM prices at the current value of po and the current value of p↑ are:

オラクル価格が一定のままであれば、AMM は通常の方法で機能します。たとえば、ETH が上昇した場合は売り、下がった場合は ETH を購入します。 x= 0 を次のように置き換えるだけです。"電流降下"PCD または y= 0 の価格は次のように置き換えられます。"電流上昇"p の価格の pcu 値を不変式にそれぞれ代入すると、po の現在値と p↑ の現在値の下での AMM 価格は次のようになります。

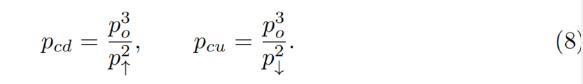
Another practically important question is: if price changes up or down so slowly that the oracle price po is fully capable to follow it adiabatically, what amount y↑ of ETH (if the price goes up) or x↓ of USD (if the price goes down) will the band end up with, given current values x and y and that we start also at p = po. While it’s not an immediately trivial mathematical problem to solve, numeric computations showed a pretty simple answer:

もう一つの重要な実践的な質問: 価格の変化が非常にゆっくりであるため、オラクル価格 po が (バンド内で) 「断熱的に」完全に追従できる場合、現在の値 x と y が与えられると、p=po のときから開始します。まず、このバンドは最終的に ETH の y↑ (価格が上がった場合) または USD の x↓ (価格が下がった場合) をどれだけ手に入れることになるでしょうか。これはすぐに解決できる数学的問題ではありませんが、数値計算により非常に簡単な答えがわかります。

We will use these results when evaluating safety of the loan as well as the potential losses of the AMM.

これらの結果は、融資の安全性と AMM の潜在的な損失を評価する際に使用されます。

Now we have a description of one band. We split all the price space into bands which touch each other with prices p↓ and p↑ so that if we set a base price pbase and have a band number n:

ここでバンドの説明をします。すべての価格空間を、価格 p↓ と p↑ が互いに接触するバンドに分割します。したがって、バンド番号 n で基準価格 pbase を設定すると、次のようになります。

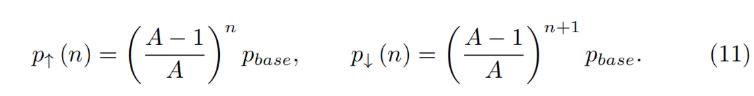
It is possible to prove that the solution of Eq. 7 and Eq. 5 for any band gives:

どの帯域についても、式 7 と式 5 の解が得られることがわかります。

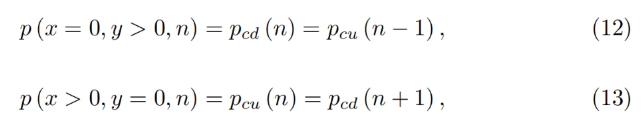
which shows that there are no gaps between the bands.

これは、バンド間にギャップがないことを示しています。

Trades occur while preserving the invariant from Eq. 1 , however the current price inside the AMM shifts when the price po: it goes up when po goes down and vice versa cubically, as can be seen from Eq. 8.

最初のレベルのタイトル

LLAMMA vs Stablecoin

Stablecoin is a CDP where one borrows stablecoin against a volatile collateral (cryptocurrency, for example, against ETH). The collateral is loaded into LLAMMA in such a price range (such bands) that if price of collateral goes down relatively slowly, the ETH gets converted into enough stablecoin to cover closing the CDP (which can happen via a self-liquidation, or via an external liquidation if the coverage is too close to dangerous limits, or not close at all while waiting for the price bounce).

ステーブルコインは、人々が揮発性担保（ETH などの暗号通貨）に対して借りる CDP の一種です。担保はLLAMMAの価格帯（バンドなど）にロードされ、担保の価格が比較的ゆっくりと下落した場合、ETHはCDPのクローズをカバーするのに十分なステーブルコインに変換されます（これは自己清算または外部清算を通じて発生する可能性があります。住宅ローン金利が危険限界に近すぎるか、価格が回復するのを待っている間はまったく近づかない）。

When a user deposits collateral and borrows a stablecoin, the LLAMMA smart contract calculates the bands where to locate the collateral.  When the price of the collateral changes, it starts getting converted to the stablecoin. When the system is “underwater”, user already has enough USD to cover the loan. The amount of stablecoins which can be obtained can be calculated using a public get_x_down method. If it gives values too close to the liquidation thresholds - an external liquidator can be involved (typically shouldn’t happen within a few days or even weeks after the collateral price went down and sideways, or even will not happen ever if collateral price never goes up or goes back up relatively quickly). A health method returns a ratio of get_x_down to debt plus the value increase in collateral when the price is well above “liquidation”.

ユーザーが担保を預けてステーブルコインを借りると、LLAMMA スマート コントラクトは担保がどのバンドにあるかを計算します。担保の価格が変化すると、ステーブルコインへの変換が開始されます。システムが入っているとき"水中"、ユーザーはローンを支払うのに十分な米ドルをすでに持っています。取得できるステーブルコインの量は、パブリックな get_x_down メソッドを通じて計算できます。清算基準値に近すぎる値を与える場合、外部の清算人が関与する可能性があります（担保価格が下落して横ばいになった後、通常は数日または数週間以内に起こるべきではありません。たとえ、担保価格がまったく上昇しなかったり、相対的に上昇が早かったとしてもです）ピックアップ、それは決して起こりません）。価格がそれよりもはるかに高い場合"清算する"、健全なメソッドは、負債に対する get_x_down の比率に加えて、担保価値の増加を返します。

When a stablecoin charges interest, this should be reflected in the AMM, too. This is done by adjusting all the grid of prices. So, when a stablecoin charges interest rate r, all the grid of prices in the AMM shifts upwards with the same rate r which is done via a base_price multiplier. So, the multiplier goes up over time as long as the charged rate is positive.

ステーブルコインが利息を請求する場合、これは AMM に反映される必要があります。それも反映されなければなりません。これは、すべてのグリッドを価格に合わせて調整することで実現されます。したがって、ステーブルコインが金利 r を課す場合、AMM 内のすべての価格は同じ金利 r で上昇し、これは基準価格乗数を介して行われます。したがって、請求されるレートがプラスである限り、乗数は時間の経過とともに増加します。

When we calculate get_x_down or get_y_up, we are first looking for the amounts of stablecoin and collateral x∗ and y∗ if current price moves to the current price po. Then we look at how much stablecoin or collateral we get if po adiabatically changes to either the lowest price of the lowest band, or the highest price of the highest band respectively. This way, we can get a measure of how much stablecoin we will which is not dependent on the current instantaneous price, which is important for sandwich attack resistance.

get_x_down または get_y_up を計算するとき、最初に探すのは、現在の価格が現在の価格 po に移動した場合のステーブルコインと担保 x∗ および y∗ の量です。次に、po が最低範囲の最低価格、または最高範囲の最高価格に断熱的に変化する場合、それぞれどれだけのステーブルコインまたは担保を取得できるかを確認します。このようにして、現在の瞬間価格に依存しない、どのくらいのステーブルコインを取得できるかの目安を得ることができます。これはメザニン攻撃への耐性にとって重要です。 **
**

It is important to point out that the LLAMMA uses po defined as ETH/USD price as a price source, and our stablecoin could be traded under the peg (ps < 1 ) or over peg (ps > 1 ). If ps < 1 , then price in the LLAMMA is p > po.

LLAMMA は価格ソースとして ETH/USD の価格として定義される po を使用し、当社のステーブルコインはペッグ以下 (ps<1) またはペッグ以上 (ps>1) で取引できることを指摘しておく必要があります。 psの場合<1 の場合、LLAMMA の価格は p>po です。

In adiabatic approximation, p = po/ps, and all the collateral<>stablecoin conversion would happen at a higher oracle price / as if oracle price was lower and equal to:

断熱近似では、p=po/ps、すべての担保<>ステーブルコインの変換は、より高いオラクル価格で、またはオラクル価格がより低く、以下に等しいかのように行われます。

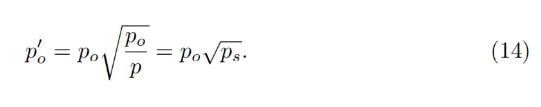
At this price, the amount of stablecoins obtained at conversion is higher by factor of 1/ps (if ps < 1 ) .

この価格では、変換時に得られるステーブルコインの数は 1/ps 倍になります (ps の場合)。<1 ）。

It is less desirable to have ps > 1 for prolonged times, and for that we will use the stabilizer (see next)

自動安定装置と金融政策

Automatic Stabilizer and Monetary Policy

自動安定装置と金融政策

When ps > 1 (for example, because of the increased demand for stablecoin), there is peg-keeping reserve formed by an asymmetric deposit into a stableswap Curve pool between the stablecoin and a redeemable reference coin or LP token. Once ps > 1 , the PegKeeper contract is allowed to mint uncollateralized stablecoin and (only!) deposit it to the stableswap pool single-sided in such a way that the final price after this is still no less than 1. When ps < 1 , the PegKeeper is allowed to withdraw (asymmetrically) and burn the stablecoin.

ps > 1の場合（例えば、ステーブルコインの需要増加により）、ステーブルコインと、ステーブルスワップ曲線プールへの償還可能な参照コインまたはLPトークンとの間の非対称デポジットによって形成されるペッグされた準備金が存在します。 ps>1 になると、PegKeeper コントラクトは無担保のステーブルコインを鋳造し、片側のステーブルスワップ プールにのみ預けることができ、その後の最終価格は依然として 1 を下回ることはありません。いつ ps1 未満の場合、PegKeeper はステーブルコインを (非対称的に) 出金および燃焼することができます。

These actions cause price ps to quickly depreciate when it’s higher than 1 and appreciate if lower than 1 because asymmetric deposits and withdrawals change the price. Even though the mint is uncollateralized, the stablecoin appears to be implicitly collateralized by liquidity in the stablecoin pool. The whole mint/burn cycle appears, at the end, to be profitable while providing stability.

これらのアクションにより、非対称の入出金によって価格が変化するため、価格 ps は 1 を超えると急速に下落し、1 を下回ると上昇します。 「鋳造」のこの部分は無担保ですが、ステーブルコインは、ステーブルコインプール内の流動性の暗黙の担保によって裏付けられているようです。安定性を提供しながら、鋳造/燃焼サイクル全体が最終的には利益をもたらすようです。

Let’s denote the amount of stablecoin minted to the stabilizer (debt) as dst and the function which calculates necessary amount of redeemable USD to buy the stablecoin in a stableswap AMM get_dx as fdx(). Then, in order to keep reserves not very large, we use the “slow” mechanism of stabilization via varying the borrow r:

ステーブルコインに鋳造されたステーブルコインの量（負債）を dst として、ステーブルスワップ AMM get_dx でステーブルコインを購入するために必要な償還可能な USD の量を計算する関数を fdx() として示します。次に、「予約」が大きくならないようにするために、次を使用します。"遅い"安定化機構。

where h is the change in ps at which the rate r changes by factor of 2 (higher ps leads to lower r). The amount of stabilizer debt dst will equilibrate at different value depending on the rate at ps = 1 r 0. Therefore, we can (instead of setting manually) be reducing r 0 while dst/supply is larger than some target number (for example, 5%) (thereby incentivizing borrowers to borrow-and-dump the stablecoin, decreasing its price and forcing the system to burn the dst) or increasing if it’s lower (thereby incentivizing borrowers to return loans and pushing ps up, forcing the system to increase the debt dst and the stabilizer deposits).

最初のレベルのタイトル

結論・まとめ

The presented mechanisms can, hopefully, solve the riskiness of liquidations for stablecoin-making and borrowing purposes. In addition, stabilizer and automatic monetary policy mechanisms can help with peg-keeping without the need of keeping overly big PSMs.

提案されたメカニズムが、ステーブルコインの鋳造と融資を目的とした清算の危険な性質に対処することが期待されています。さらに、スタビライザーと自動金融政策メカニズムは、過剰な PSM (ペグ安定モジュールアンカー安定モジュール) を維持する必要なく、価格アンカーを維持するのに役立ちます。