DAOrayaki：優化二次方融資，利用SGD實現顯示原理（附機制資源集）
原文作者: Ethereum
原文作者: Ethereum
原文標題: Quadratic Funding: Implementing the revelation principle using SGD
我們認為，在這種情況下，如果有良好的圖形界面，直接近似顯示（direct approximate revelation）對用戶來說更簡單，因此進一步增加了生產性協調難度和非生產性協調難度之間的差距。我們描述了一個近似啟發過程（approximate elicitation procedure），參考了Critch 2022[4] 以及一個使用隨機梯度下降(SGD) 的策略執行器（strategy executor），儘管我們可以使用任何全局優化算法，例如Adam[ 5]、 Adagrad[6]等。然後我們討論計算可行性以及如何使策略執行器無需信任和/或保持隱私。
想要進一步了解二次方融資機制背景及相關實踐和研究，可查看文末參考文獻，DAOrayaki去中心化編輯委員會對二次方機制特作整理。
標準QF 策略中的信息挑戰
Buterin、Weyl 和Hitzig（2018 年）[7] 指出，“動態實施很可能是可取的[...]，因為最佳貢獻仍將取決於其他人的貢獻”。換句話說，除非我知道別人貢獻了多少，否則我不知道貢獻多少，但除非他們知道我貢獻了多少，否則其他人不知道貢獻多少。但老實說，我不會經常登錄來檢查和調整我的分配。
讓我們說明如果只是簡單地呈現匹配（match）的靜態預計（可能會歪曲最終匹配）會發生什麼。每個項目將從$0 的靜態匹配開始。第一個收到貢獻的項目將跳轉到100% 預算的靜態匹配。這會隨著時間的推移而稀釋，但最初的影響是如此之大，以至於它很可能會持續存在，即實際上，被“吸引”來的參與者不會作二次檢查然後退出。
直觀的結論是，“先行者”（first mover）對公共物品的結果具有不成比例的影響（這可能會因與UI 排序等相關的先行者優勢而加劇）。 Gitcoin 的相關數據[8] 初步表明，可能確實存在先行者優勢（是否有因果關係需要進一步分析）。
我們能想出一個“智能”預計嗎？這樣的努力可能會面臨全信息限制（full-information constraint），引入中心化的嚴重偏見，或兩者兼而有之。
顯示原理
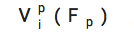顯示原理（Revelation Principle）[9]指出，對於任何機制m1都有一個“直接機制” m2，直接詢問代理人的偏好並為他們執行策略。是否m2比m1更有用，取決於偏好的描述長度（組合拍賣可以作為一個例子[10]， 我們通常不想要直接機制）。在QF 這裡，完整的偏好描述是一個連續函數
；但是，我們可以近似指定此函數為一維或二維的一些數據點。請注意，我們不考慮聯合效用，因為這會增加描述長度；所以，這更適用於相對獨立的商品或單一商品的博弈。 （見後續文章[11]）
啟發（Elicitation）
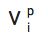
我們有無數的方法來改善用戶界面（UI），但一個簡單的界面可能是一個基於點擊/拖動的界面，人們可以拖動和/或鍵入一些
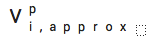
的值。另一個可能是“批量價格”用戶界面，用戶可以對我們的“批量折扣”出價，直到他們滿意為止。我們還向用戶解釋，他們在項目上花費的金額永遠不會超過他們給我們的個人估值。然後我們將使用任何常見的插值方法[9]並將結果
提交給策略執行器（strategy executor）。請注意，如果給定項目的總邊際效用近似值偏離，則該項目可能資金不足或資金過剩，因為邊際社會效益(MSB) 將與其他項目相差k。我們預計，隨著越來越多的人報告一個給定項目，隨機錯誤近似值（random mis-approximation）將平均化。
這個例子有助於你建立概念，標準QF 在用戶每次登錄時都會重新查詢用戶的出價，因為匹配金額會不斷變化。此UI 會預先查詢一個最少的出價集。
該方案類似於Critch 2022[9] 中介紹的，這也表明一個討論組件（discussion component）比啟發本身更重要。請注意，Critch 2022 通常預設的是高度敬業的個體子集，試圖代表整個世界的效用，而不是茫茫多不那麼敬業的自私代理人（請注意，任何有效的公共物品募資計劃都可能具有前者的一些屬性，因為有利於非選民（例如遙遠的甚至不遠的未來公民）的項目需要無私，並且參與/奉獻也遵循80/20[10] 法則）。 Critch 的觀點是有道理的，儘管進一步的討論超出這篇文章的範圍。
優化
用戶將授權一些支付給機器人，然後機器人將運行梯度下降（gradient descent），模擬用戶在頻繁檢查和調整分配時可能會做的事情。
Buterin、Weyl 和Hitzig (2018) 還指出，非凹效用（nonconcave utility）是自然的，但會使系統的吸引子非全局（例如“冷啟動”效用曲線- 可視化[11]）。因此，我們可以通過使用梯度下降/全局最優化的隨機（stochastic） 變種來實現收益，從這個意義上說，SGD 也可以作為一種策略修改來誘導相關均衡[12]。
在機制中使用區塊鏈-SGD-協調器可能是一個更廣泛的加密經濟研究領域。例如，代理人對損失函數的選擇（例如， 羅爾斯vs.功利主義[13]）會影響它選擇的均衡[14]（ 民間定理[15] 表明均衡選擇在許多情況下都很重要），這可能使設計者能夠控制[16] 效率與公平、風險與收益等。一個自然的問題是，人們在同一場遊戲（博弈） 的不同協調者之間選邊站，元遊戲是否會因此產生。
均衡選擇問題與維度災難有關——吸引子的數量和發現它們的難度可能會因人數而急劇增加。我們現在正在優化具有超過數千億參數的深度學習模型的事實讓我們感到欣慰，儘管這種規模的優化成功可能涉及各種前沿技術和手動調整。我們預計優化超過數千到數百萬的貢獻量不會有很大的問題，特別是如果空間確實是凹的，而且考慮到問題的本質不是黑匣子，我們可以對起點做出有根據的猜測。然而，一旦我們需要證明，計算就會突然變得昂貴起來（鑑於這樣的限制，非虛擬化Cosmos[17] 區塊鏈的共識層計算——如果擴展性足夠好，可能帶有欺詐證明——可能是不那麼雄心勃勃的起點）。我們強調，如果參與者在心理上執行，SGD 算法面臨的任何優化挑戰將更加嚴峻（例如，我們認為即使在最簡單的場景中，參與者也不太可能發現均衡）。
如果我們使用報告估值的線性插值，離散優化也可能提供優化。我們不需要沿著梯度下降，而是在點之間移動。
交互複雜度
公共物品的性質是，每個物品i 都與每個參與者j 相關。因此，系統的交易成本是X * Y * K，其中X = 人口，Y = 公共物品選項的數量，K = 交易成本。我們認為，進入效用曲線的K 低於使用直接貢獻博弈的K，如果UI 設計沒毛病，K 基本上是最小的，瓶頸是X * Y。由於激勵的原因，降採樣X 可能不可行，而對Y 的隨機降採樣的改進可能來自同行評審、搜索和個性化推薦。
同意、無需信任和隱私
因為我們授權機器人替我們花錢，所以我們必須強制機器人做正確的事情。這是一個共識和/或證明的用例（儘管可能很貴，參見前面關於計算成本的說明）。
我們也可能希望輸入和個人分配是隱私的。 SGD 方法實際上更適合差分隱私（這是同態閾值加密的一個用例[18]），因為計算本質上是最大批量的（maximally batched），即總的最終分配可以直到最後才揭曉。在直接貢獻的情況下，我們必須定期更新分配估計（從技術上講，這做不到，但不這樣做，博弈會變成只有一次機會，因此無法玩），這暴露了更新頻率和隱私之間的權衡。
鑑於這種隱私能力，我們可能想重新審視MACI 匿名化[19]。
心理學
有人可能會爭辯說，看到一場巨大的和/或誇大的匹配預計，能讓人享受參與QF 的樂趣，比起潛在的機制最優化的扭曲，這是值得的，並且/或者機制的最優化在實踐中是一個不切實際的目標（例如，“效用”不是一個清晰的概念）。如果該機制的很大一部分吸引力實際上是其心理效應而不是博弈論效應，那麼我們仍然可以報告預計匹配（當然，這將重新引入前面提到的更新頻率權衡）。
混合系統
參考文獻
參考文獻
參考文獻
1.DAOrayaki Podcast ｜二次方治理規模化的現實約束與解法探索
7. DAOrayaki ｜從默認選擇到二次方投票:投票一覽
8. DAOrayaki｜二次方投票：機制設計如何使民主激進化
12. 二次方資助V2協議: 抗女巫攻擊、公平和規模化的鏈上二次方投票
14. 13. Dora Factory Eric Zhang：使用累進稅系統提高二次方資助的公平性
15. 二次方融資（Quadratic Funding）的攻擊與防守
社會實驗| 讓社區資助爆發巨大能量，當二次方投票遇上黑客馬拉松
尾註
https://anvaka.github.io/fieldplay/?cx=0480000000000005&cy=3.0061&w=13.711400000000001&h=13.711400000000001&dt=0.01&fo=0.998&dp=0.009&cm=1&vf=%2F%2F%20alpha%20%3D%200.5%2C%20V_i%5Ep%28F_p%29%20%3D%20arctan%28F_p%29%0Avec2%20get_velocity%28vec2%20p%29%20%
https://anvaka.github.io/fieldplay/?cx=9.78905&cy=7.32765&w=32.5177&h=32.5177&dt=0.01&fo=0.998&dp=0.009&cm=1&vf=%2F%2F%20Prisoner%27s%20Dilemma%3A%20alpha%20%3D%200.5%2C%20V_i%5Ep%28F_p%29%20%3D%20F_p%20%2F%202%0Avec2%20get_velocity%28vec2%20p%29%20%7B%0A%
https://www.wolframalpha.com/input?i=3d+plot+0.5%280.5%28sqrt%28x%29+%2B+sqrt%28y%29%29%5E2+%2B+0.5x%29+-+x+and+0.5%280.5%28sqrt%28x%29+%2B+sqrt%28y%29%29%5E2+%2B+0.5y%29+-+y%2C+x+from+0+to+1%2C+y+from+0+to+1
https://www.youtube.com/watch?v=yDJ5KiZx7Yw
https://optimization.cbe.cornell.edu/index.php?title=Adam
https://optimization.cbe.cornell.edu/index.php?title=AdaGrad
https://arxiv.org/abs/1809.06421
https://gov.gitcoin.co/t/improving-grant-matching-estimates-during-the-round/7809/3
https://www.youtube.com/watch?v=yDJ5KiZx7Yw
https://en.wikipedia.org/wiki/Pareto_principle
https://anvaka.github.io/fieldplay/?cx=9.78415&cy=6.979699999999999&w=32.5079&h=32.5079&dt=0.01&fo=0.998&dp=0.009&cm=1&vf=%2F%2F%20alpha%20%3D%201.%2C%20V_i%5Ep%28F_p%29%20%3D%205%28arctan%28F_p%20-%2010%29%20-%20arctan%28-10%29%29%0Avec2%20get_velocity%28
https://en.wikipedia.org/wiki/Correlated_equilibrium
https://ocw.mit.edu/courses/14-01-principles-of-microeconomics-fall-2018/88b8835701f40269b3fb5b5e537179a3_MIT14_01F18_lec18_25.pdf
https://en.wikipedia.org/wiki/Equilibrium_selection
https://en.wikipedia.org/wiki/Folk_theorem_(game_theory)
https://www.goodreads.com/quotes/82034-he-who-controls-the-spice-controls-the-universe
https://docs.cosmos.network/main/intro/overview.html
https://protocol.penumbra.zone/main/crypto/flow-encryption/threshold-encryption.html
https://ethresear.ch/t/maci-anonymization-using-rerandomizable-encryption/7054
https://ethresear.ch/t/quadratic-funding-optimal-incremental-revelation-for-the-multi-good-case/13109
