Tiếp nối chương trước, chúng tôi đã xuất bản bốn bài viết trong loạt bài về Xây dựng danh mục tài sản tiền điện tử mạnh mẽ bằng cách sử dụng mô hình đa yếu tố:Cơ sở lý thuyết、Tiền xử lý dữ liệu、Kiểm tra tính hợp lệ của yếu tố、Phân tích nhân tố danh mục lớn: Tổng hợp nhân tố。

Ở bài trước chúng tôi đã giải thích chi tiết về vấn đề cộng tuyến nhân tố (tương quan cao giữa các nhân tố), trước khi tổng hợp các loại nhân tố lớn, cần phải thực hiện trực giao nhân tố để loại trừ hiện tượng cộng tuyến.

1. Đạo hàm toán học của trực giao nhân tử

Từ góc độ hồi quy cắt ngang đa yếu tố, một hệ thống trực giao nhân tố được thiết lập.

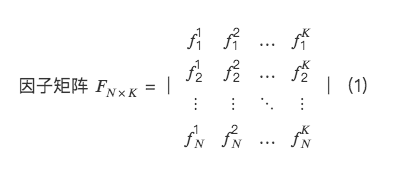
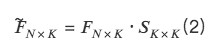
Vì thế,

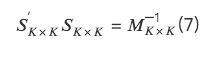
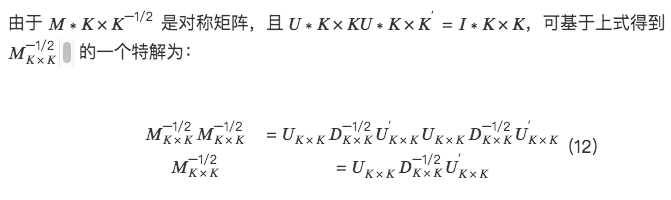
2. Cụ thể thực hiện ba phương pháp trực giao

1.Schmitt trực giao

Trực giao Schmidt là một phương pháp trực giao tuần tự nên cần phải xác định thứ tự trực giao của nhân tử, thứ tự trực giao thông thường bao gồm thứ tự cố định (cùng một thứ tự trực giao được lấy trên các phần khác nhau) và thứ tự động (thứ tự trực giao giống nhau được lấy trên mỗi phần). phần) Thứ tự trực giao được xác định theo những quy tắc nhất định). Ưu điểm của phương pháp trực giao Schmidt là có sự tương ứng rõ ràng giữa các yếu tố trực giao trong cùng một thứ tự, tuy nhiên, không có tiêu chuẩn lựa chọn thống nhất cho thứ tự trực giao, hiệu suất sau khi trực giao có thể bị ảnh hưởng bởi tiêu chuẩn thứ tự trực giao và thời gian cửa sổ thông số. .

2. Tính trực giao thông thường

# Canonical trực giao def Canonical(self):
 overlapping_matrix = (time_tag_data.shape[ 1 ] - 1) * np.cov(time_tag_data.astype(float))
# Lấy giá trị riêng và vectơ riêng
 eigenvalue, eigenvector = np.linalg.eig(overlapping_matrix)
# Chuyển đổi sang ma trận trong np
 eigenvector = np.mat(eigenvector)
 transition_matrix = np.dot(eigenvector, np.mat(np.diag(eigenvalue ** (-0.5))))
 orthogonalization = np.dot(time_tag_data.T.values, transition_matrix)
 orthogonalization_df = pd.DataFrame(orthogonalization.T, index = pd.MultiIndex.from_product([time_tag_data.index, [time_tag]]), columns=time_tag_data.columns)
 self.factor_orthogonalization_data = self.factor_orthogonalization_data.append(orthogonalization_df)

3. Trực giao đối xứng

Do trực giao Schmidt áp dụng cùng thứ tự trực giao của các thừa số trên một số phần trước, nên có sự tương ứng rõ ràng giữa các thừa số trực giao và các thừa số ban đầu, trong khi trực giao chính tắc chọn các thành phần chính trên mỗi phần. sự tương ứng ổn định giữa các yếu tố trước và sau trực giao. Có thể thấy, tác động của tổ hợp trực giao phụ thuộc phần lớn vào việc có sự tương ứng ổn định giữa các yếu tố trước và sau trực giao hay không.

Tính trực giao đối xứng làm giảm các sửa đổi đối với ma trận nhân tố ban đầu càng nhiều càng tốt để thu được một tập hợp các cơ sở trực giao. Điều này có thể duy trì sự tương đồng giữa các yếu tố trực giao và các yếu tố nguyên nhân ở mức độ lớn nhất. Và tránh ưu tiên các yếu tố sớm hơn theo thứ tự trực giao như phương pháp trực giao của Schmidt.

Tính chất trực giao đối xứng:

1. So với trực giao Schmidt, trực giao đối xứng không cần cung cấp thứ tự trực giao và xử lý từng yếu tố như nhau.

2. Trong số tất cả các ma trận chuyển tiếp trực giao, độ tương đồng giữa ma trận trực giao đối xứng và ma trận gốc là lớn nhất, tức là khoảng cách giữa các ma trận trực giao trước và sau là nhỏ nhất.