ห้านาทีเพื่อทำความเข้าใจอัลกอริทึม PMM ที่อยู่เบื้องหลัง DODO: กรอบสภาพคล่องทั่วไปและกรณีการ
ตลาดที่มีประสิทธิภาพประกอบด้วยข้อมูลจำนวนมหาศาล ซึ่งใช้ตัดสินราคาของตลาด อย่างไรก็ตาม ทรัพยากรการประมวลผลบน chain มีจำกัด การตระหนักถึงตลาดที่มีความยืดหยุ่นสูงบน chain นั้นเหมือนกับการยัดช้างเข้าไปในตู้เย็น
การยัดช้างไว้ในตู้เย็นไม่ใช่เรื่องแปลก และในประวัติศาสตร์ของอินเทอร์เน็ตมีความสำเร็จหลายอย่าง เช่น การบีบอัดภาพ การบีบอัดเสียง
สาระสำคัญของการบีบอัดคือการดึงคุณลักษณะที่สำคัญที่สุดและละทิ้งรายละเอียดที่ไม่สำคัญ
ดังนั้น คุณลักษณะที่สำคัญที่สุดของตลาดคือสภาพคล่อง สภาพคล่องสามารถแสดงเป็นแผนผังเชิงลึกได้
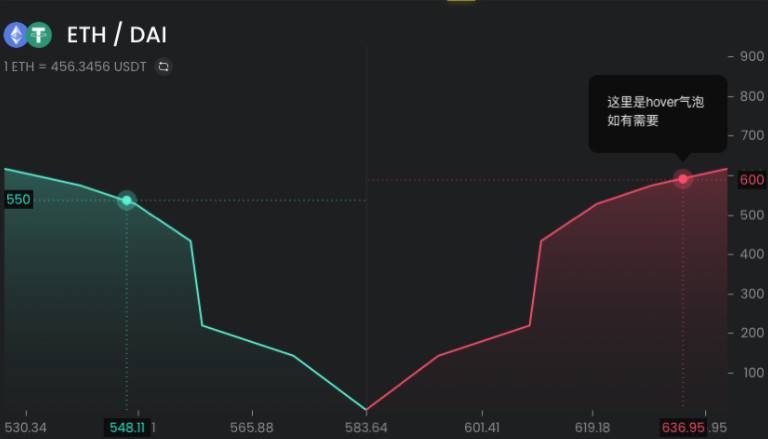
จากรูปด้านล่าง เราจะเห็นว่าแผนที่ความลึกสามารถสรุปเป็นรูปสามเหลี่ยมสองรูปได้ และเพื่ออธิบายรูปสามเหลี่ยมทั้งสองนี้ จำเป็นต้องใช้เพียงค่ามัธยฐานและความชันเท่านั้น
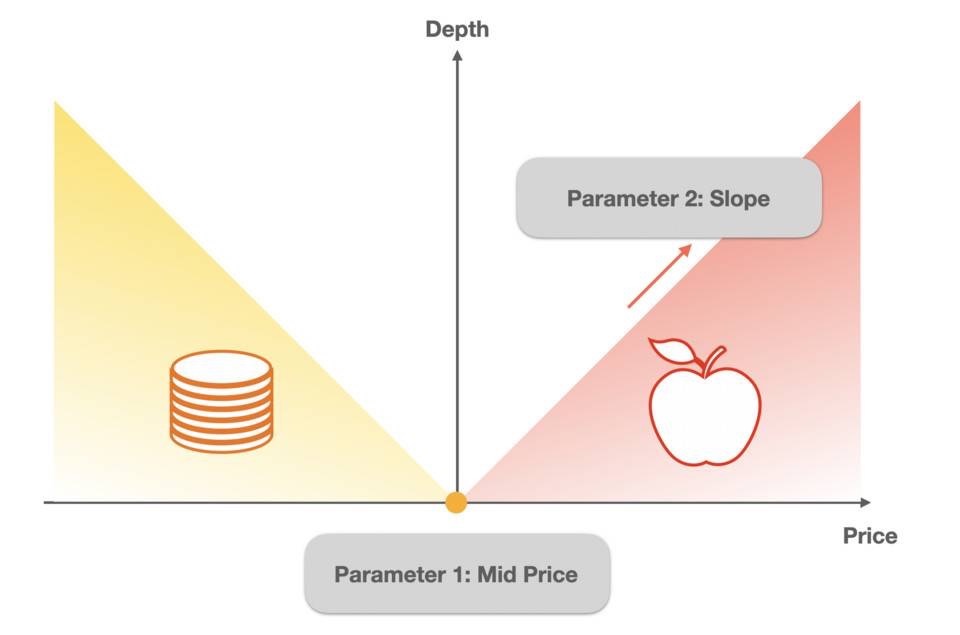
เรามุ่งเน้นไปที่ความลึกของการขายรูปสี่เหลี่ยมคางหมู ทางด้านขวา คุณลักษณะที่ใหญ่ที่สุดของมันคือ ยิ่งซื้อ Base Token มาก ราคาก็จะยิ่งสูงขึ้น ดังนั้นความลึกเชิงเส้นนี้สามารถแสดงเป็น
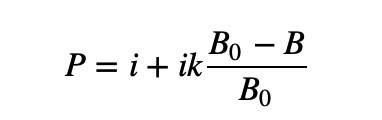
โดยที่ i คือพารามิเตอร์ตัวแรก "ราคากลาง" และ k คือพารามิเตอร์ตัวที่สอง "slope"
B แสดงถึงคลังโทเค็นฐานปัจจุบัน B0 แสดงถึงคลังโทเค็นฐานเริ่มต้น และ (B0-B)/B0 ใช้เพื่อระบุเปอร์เซ็นต์ของ BaseToken ที่ใช้ไป
สูตรนี้สามารถทำให้ราคาเพิ่มขึ้นเป็นเชิงเส้นกับจำนวนของ Base Token ที่ขายได้
แต่เส้นตรงเป็นวิธีที่ดีที่สุดในการอธิบายความคล่องตัวหรือไม่? ไม่ คำอธิบายเชิงเส้นมีข้อจำกัดสองประการ:
1. ในตลาดจริง สภาพคล่องส่วนใหญ่กระจุกตัวอยู่ใกล้ราคากลางของตลาด และคำอธิบายเชิงเส้นไม่ได้สะท้อนถึงการกระจายที่ไม่สมดุลนี้
2. แม้ว่าราคาจะเบี่ยงเบนไปจากราคากลางของตลาดมาก แต่ก็ควรมีสภาพคล่อง และราคาภายใต้คำอธิบายเชิงเส้นจะมีขีดจำกัดบนและล่าง
เราแนะนำความไม่เชิงเส้นให้กับเส้นโค้งราคา บนพื้นฐานของการไม่ขยายพารามิเตอร์ การกระจายเชิงลึกจะสอดคล้องกับกฎของตลาดมากกว่าและมีความยืดหยุ่นสูงกว่า
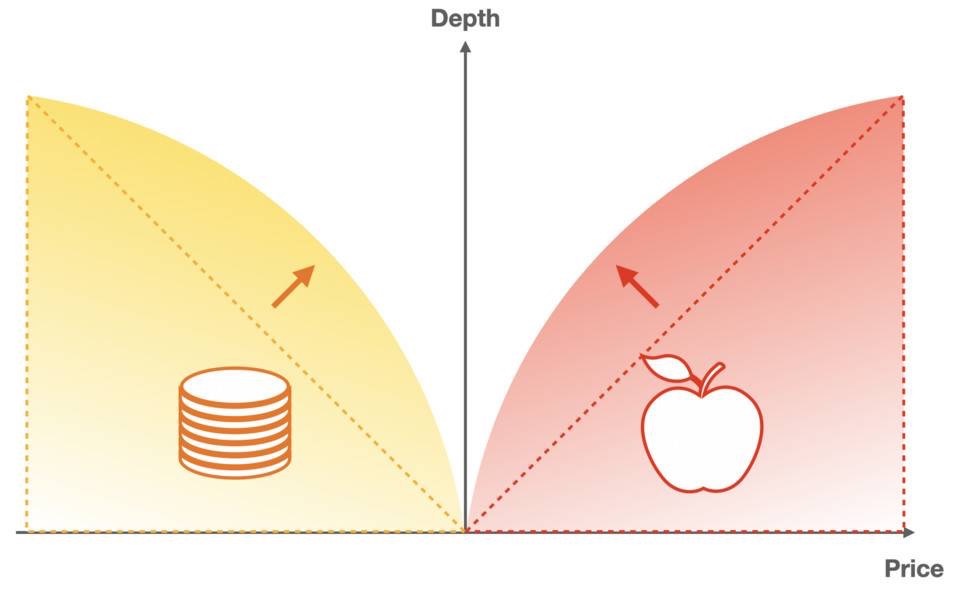
วิธีการแก้ปัญหาที่ไม่ใช่เชิงเส้นที่ง่ายที่สุดคือการใช้การคูณแทนการบวก
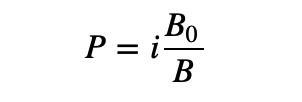
สูตรนี้สามารถตอบสนองได้ว่าเมื่อ B ลดลง P จะเพิ่มขึ้นเรื่อย ๆ จนถึงอนันต์ แต่คุณจะเพิ่มเอฟเฟกต์ของความชันได้อย่างไร?
สิ่งนี้จำเป็นต้องมีการแก้ไขรายการ B0/B B0/B≥1 เราใช้พารามิเตอร์เพื่อปรับขนาด ขณะที่รักษาค่านี้ให้มากกว่าหรือเท่ากับ 1 เราสามารถควบคุม "ระดับที่มากกว่า 1" ได้
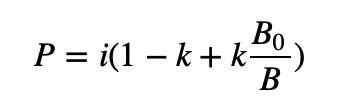
ในสูตรข้างต้น ช่วงของค่า k คือ [0,1] ซึ่งกำหนดความชันของราคา
เมื่อ k=0 ราคาจะไม่เปลี่ยนแปลงโดยสิ้นเชิง
เมื่อ k=1 ความชันของราคาจะลดระดับลงเป็นเวอร์ชันก่อนหน้าของสูตร
ค่า k ยิ่งมาก ยิ่งไวต่อการเปลี่ยนแปลงของราคา ค่า k ที่น้อยกว่าคือความไวต่อการเปลี่ยนแปลงของราคาน้อยกว่า
แต่ก็ยังมีปัญหาเล็กน้อย โดยที่ P คือราคาส่วนเพิ่ม และค่าอินทิกรัลของราคาส่วนเพิ่มคือจำนวนสินทรัพย์ที่ผู้ใช้ต้องจ่าย ในสูตรข้างต้น ฟังก์ชันลอการิทึมจะปรากฏขึ้นหลังจากอินทิกรัลของ B0/B ซึ่งจะทำให้การคำนวณที่ตามมาซับซ้อนมาก เพื่อหลีกเลี่ยงปัญหานี้ เราก้าวไปอีกขั้นหนึ่ง:
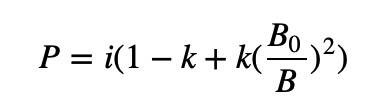
เพิ่มเทอมสแควร์นอก B0/B เพื่อให้หลังจากการรวมจะกลายเป็นการหารอย่างง่าย
น่าแปลกที่เมื่อ k=1 เส้นโค้งนี้เป็นเส้นโค้งพันธะที่กำหนดโดย AMM ความบังเอิญนี้ทำให้เราเชื่อว่านี่คือชุดของอัลกอริทึมที่สัมผัสแก่นแท้ของตลาดมากขึ้น
ในทำนองเดียวกัน สำหรับแผนที่ความลึกในครึ่งซ้าย เราใช้วิธีการแบบสมมาตรเพื่อแทนที่โทเค็นฐานด้วยโทเค็นใบเสนอราคา และแทนที่การคูณด้วยการหาร:
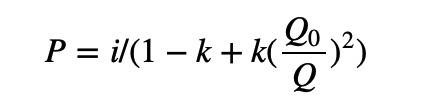
เรารวมแผนที่ความลึกทางด้านซ้ายและด้านขวาเพื่อให้ได้อัลกอริทึม PMM เวอร์ชันสมบูรณ์ เรียงลำดับ:

อัลกอริทึม PMM เป็นตลาดคำสั่งซื้อที่มีการบีบอัดสูงพร้อมพารามิเตอร์ที่เรียบง่าย แต่มีความยืดหยุ่นสูง
สิ่งนี้ช่วยให้เรามีพลังช้างในพื้นที่ขนาดเล็กในตู้เย็น
ให้ฉันแสดงรายการกรณีการใช้งานที่อัลกอริทึมนี้สามารถทำได้โดยการปรับพารามิเตอร์และกฎการฝากและถอน
ใช้กรณีที่ 1 การสร้างตลาดที่ใช้งานอยู่ตามราคาตลาดภายนอก
สถานการณ์การใช้งานของกรณีการใช้งานนี้เป็นสกุลเงินหลักที่มีตลาดภายนอกขนาดใหญ่ เช่น ETH, BTC เป็นต้น
PMM สามารถตระหนักถึงการปรับราคาแต้มต่อและลด IL รับอัตราการใช้เงินทุนที่สูงกว่า AMM และถือครองสกุลเงินเดียวเพื่อให้มีสภาพคล่อง
การตั้งค่ามีดังนี้:
กำหนดราคา i เป็นราคาตลาดภายนอก
กำหนด k เป็นจำนวนที่น้อยกว่า 1
อนุญาตให้ทุกคนฝากและถอนฝ่ายเดียว
เราเรียกสิ่งนี้ว่า Use Case DODO Classic Pool
ใช้กรณีที่ 2 อัลกอริทึมการสร้างตลาดอัตโนมัติสำหรับความต้องการเงินทุนเล็กน้อย
กรณีการใช้งานนี้ใช้กับตลาดสกุลเงินหางยาวโดยไม่มีอำนาจการกำหนดราคาตามอัตวิสัย และอำนาจในการกำหนดราคาจะมอบให้กับผู้รับโดยสมบูรณ์
โดยทั่วไปแล้ว เหรียญหางยาวเป็นสินทรัพย์ใหม่ และไม่มีสภาพคล่องในการขายเพียงพอภายใต้กรอบ AMM ส่งผลให้ขาดสภาพคล่องในระยะยาว
การตั้งค่ามีดังนี้:
ตั้งราคา i เป็นราคาเริ่มต้น
ตั้งค่า k ตามอำเภอใจ
การเติมเงินครั้งแรกสามารถอยู่ในอัตราส่วนสินทรัพย์ใดก็ได้โดยไม่ต้องเปลี่ยนราคาตลาด
การเติมเงินในภายหลัง (หรือการถอนเงินสด) ต้องดำเนินการสินทรัพย์ทั้งสองในเวลาเดียวกันตามอัตราส่วนสินทรัพย์หมุนเวียน
เราเรียกสิ่งนี้ว่า Use Case DODO Vending Machine
ใช้กรณีที่ 3 อัลกอริทึมการทำการตลาดฟรีโดยสิ้นเชิง
กรณีการใช้งานนี้มีไว้สำหรับผู้ดูแลสภาพคล่องที่มีความทะเยอทะยานและต้องการสร้างความแตกต่างอย่างมาก (ผู้ดูแลสภาพคล่องสามารถเป็นบุคคลในโครงการหรือบุคคลธรรมดาได้)
ตัวอย่างเช่น:
ตัวอย่างเช่น:
สร้างตลาดประมาณ ETH=700USDT ใช้ k ขนาดเล็กมากเพื่อให้ได้สภาพคล่องที่แข่งขันได้ และรับค่าธรรมเนียมการจัดการจำนวนมาก เมื่อตรวจพบว่า ETH คาดว่าจะเพิ่มขึ้น สินค้าคงคลัง ETH จะถูกถอนออกเพื่อลดความเสี่ยงฝ่ายเดียว แต่การดำเนินการนี้ไม่ได้ทำให้สภาพคล่องในการซื้อลดลง
ฝ่ายโครงการออกสินทรัพย์ใหม่ให้โทเค็นเท่านั้น แต่ไม่ให้เงินทุน การขายโทเค็นเริ่มต้นที่ 1$ เพื่อให้ผู้คนจำนวนมากขึ้นสามารถซื้อโทเค็นได้ในราคาที่เหมาะสม ค่า k ที่เล็กกว่าจะถูกตั้งค่าเพื่อให้โทเค็นเพิ่มขึ้นในระดับปานกลาง ต่อมาเมื่อฝ่ายโครงการพบว่าจำเป็นต้องใช้เงิน ก็สามารถถอนสินทรัพย์ในกองทุนรวมได้โดยตรงโดยไม่ทำลายสภาพคล่องของคำสั่งขาย นั่นคือผู้ใช้ยังสามารถซื้อโทเค็นราคาถูกจำนวนมากได้
การตั้งค่ามีดังนี้:
เฉพาะผู้ดูแลสภาพคล่องเท่านั้นที่สามารถฝากและถอนได้ อนุญาตให้ดำเนินการในสกุลเงินเดียว
เราเรียกสิ่งนี้ว่า Use Case DODO Private Pool
ใช้กรณีที่ 4 การระดมทุนสภาพคล่อง
เราสามารถแบ่งการออกสินทรัพย์ใหม่ออกเป็นสองช่วง:
1. อย่าเปิดการซื้อขายทันที ทุกคนที่เข้าร่วมในการขายจะได้รับโทเค็นในราคาเดียวกัน
2. เริ่มธุรกรรมสปอตที่ราคาสุดท้ายของสเตจก่อนหน้า และใช้โทเค็นและสินทรัพย์ที่เหลือจากสเตจก่อนหน้าเพื่อสร้าง DODO Vending Machine
เราเรียกสิ่งนี้ว่า Use Case CrowdPooling
ใช้กรณีที่ 5 เสื่อมเป็น AMM
อัลกอริทึม PPM ทำงานเหมือนกับ AMM เมื่อตรงตามเงื่อนไขต่อไปนี้
ตั้ง k=1
ต้องฝากและถอนสินทรัพย์ทั้งสองรายการพร้อมกันตามอัตราส่วนราคาปัจจุบัน
นอกจากนี้ยังหมายความว่า AMM เป็นกรณีพิเศษของ PMM กระบวนการรับมีดังนี้:
สูตรราคาของ AMM คือ xy = k โดยที่ k คือค่าคงที่ และ x และ y แทนปริมาณของโทเค็นทั้งสองตามลำดับ เพื่อหลีกเลี่ยงความกำกวมในตัวอักษร เรากำหนดผลคูณคงที่ในสูตร AMM เป็น Const และเขียนใหม่เป็น y=Const/x
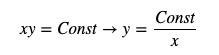
ในหมู่พวกเขา y แทนโทเค็นราคาอ้างอิง x แทนสต็อกของโทเค็นพื้นฐาน และราคาสามารถเขียนเป็นอนุพันธ์ของ y ได้ (โปรดทราบว่าต้องบวกค่าสัมบูรณ์ที่นี่ เนื่องจากราคาเป็นจำนวนบวก)
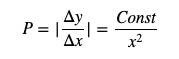
กลับไปที่สูตร PMM สำหรับ k=1 เราสามารถเขียนเป็น:
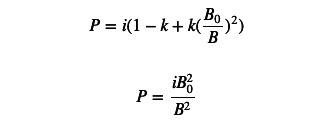
เราพบว่าตัวเศษของสูตรราคา PMM เป็นค่าคงที่ และตัวส่วนคือสต็อกของโทเค็นฐาน ตราบใดที่คำสั่ง
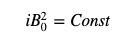
สูตรการกำหนดราคาของ AMM สอดคล้องกับสูตรการกำหนดราคาของ PMM!
ใช้กรณีที่ 6 การซื้อขาย Stablecoin
การตั้งค่ามีดังนี้:
i=1
k=0.001 (ค่ายิ่งน้อย ยิ่งใกล้เคียงกับการแลกเปลี่ยน Stablecoins ที่เข้มงวดมากขึ้น)
ประสิทธิภาพของอัลกอริทึมสามารถเหมือนกับของเส้นโค้งและมีความยืดหยุ่นมากกว่า อาจใกล้เคียงกับการแลกเปลี่ยนแบบเข้มงวดมากกว่าเส้นโค้ง หรือใกล้เคียงกับ AMM
เขียนโดย: Radar Bear ผู้ก่อตั้ง DODO



