Vị trí của Uni v3 LP có thể được chia nhỏ thành các thành phần năng suất và phạm vi.
Giá trị của vị trí Uni v3 là tổng của: 1) tổng của các vị trí bán, có giá trị được đưa ra bởi mô hình Black-Scholes; 2) thuật ngữ phạm vi, có biểu thức đóng được đưa ra bởi công thức Feynman-Kac.
Điều này có thể được đơn giản hóa hơn nữa bằng cách chuyển đổi vị trí Uni v3 LP thành quyền chọn bán "DTE cố định" có giá trị khi hết hạn hội tụ với quyền chọn bán tại thời điểm T_r > 0.
So sánh khoản hoàn trả dự kiến của một vị trí Uni v3 với phí tùy chọn có thể giúp xác định xem việc giữ một vị trí Uni v3 có lợi hơn hay cho người mua quyền chọn "vay" nó.
Để thiết lập vị trí Uniswap v3 LP, một tài sản (ví dụ: ETH) phải được khóa trong phạm vi do người dùng chỉ định (được xác định bởi tL quy mô thấp và tH quy mô cao). Giá trị của vị trí Uniswap v3 LP là:
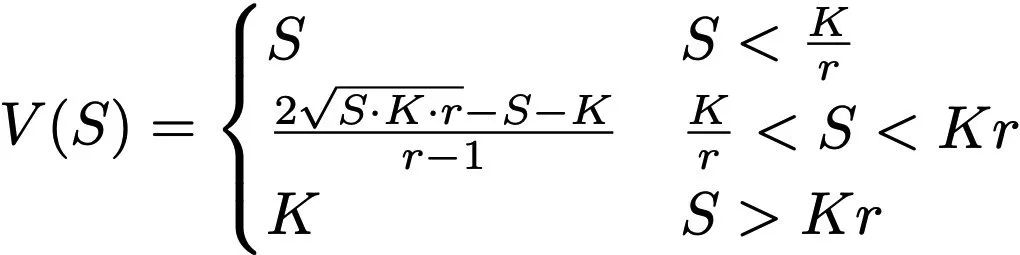
Trong số đó, S là giá tiền mặt của tài sản, K là giá thực hiện √(tL*tH), r là hệ số phạm vi √(tH/tL). Yếu tố phạm vi xác định mức độ "sắc nét" của quá trình chuyển đổi giữa các khoản giữ và số.
Điều gì về các tùy chọn dài? Nếu một người có thể mượn một vị trí Uni v3 LP và trả lại sau, thì điều đó tương đương với việc mua một quyền chọn bán. Người dùng sẽ trả một khoản phí cố định khi mượn các vị trí LP.
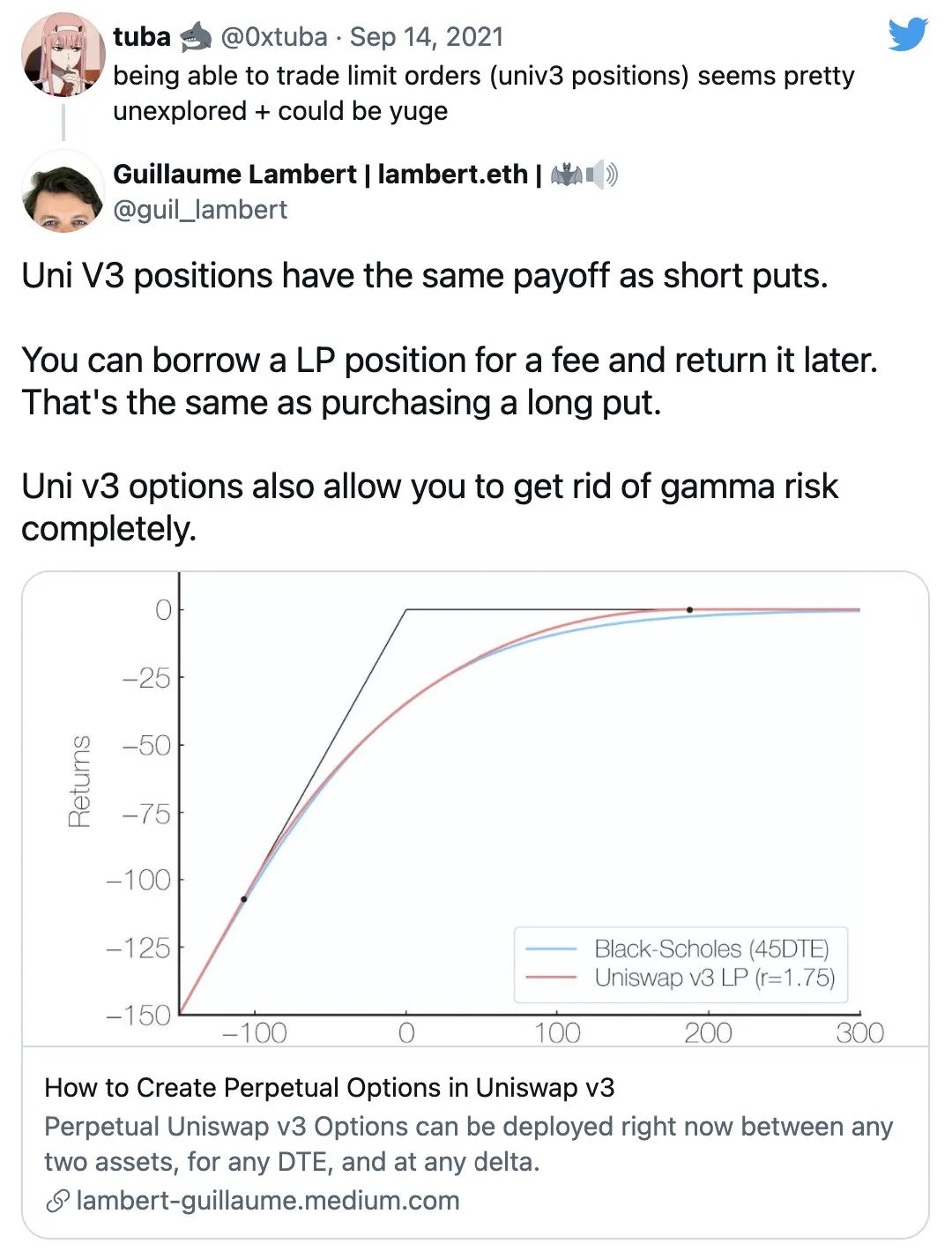
Câu trả lời là có.
Câu trả lời là có.
tiêu đề cấp đầu tiên
Định giá quyền chọn Feynman-Kac
Trước khi xác định giá của các tùy chọn Uni v3, bạn nên xem lại cách định giá các tùy chọn thông thường. Sử dụng mô hình Black-Scholes, có một số cách để xác định giá của một quyền chọn mua thông thường. Phương pháp yêu thích của tôi là sử dụng công thức Feynman-Kac, công thức này nói rằng tùy chọn u(S,t) có giá trị:
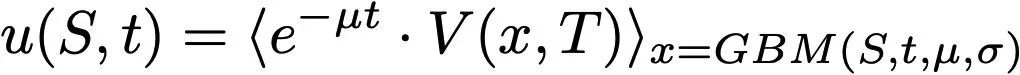
trong đó V(x, T) là hàm hoàn trả khi đáo hạn và trung bình ⟨ ⋅ ⟩ là thước đo xác suất cho chuyển động Brown hình học.
Hiểu ý nghĩa của công thức Feynman-Kac rất đơn giản: giá trị của một quyền chọn tại thời điểm T được xác định bằng cách tính giá trị trung bình của hàm hoàn trả của tất cả các thay đổi giá có thể xảy ra từ bây giờ đến thời điểm T trong tương lai.
Nhà vật lý Richard Feynman ban đầu đề xuất một phương trình tương tự ở dạng đường tích phân của cơ học lượng tử, trong đó vị trí "dự kiến" của một hạt được xác định bằng tổng trọng số của tất cả các đường khả dĩ mà hạt đó có thể đi. Mark Kac nhận ra rằng họ đang giải quyết một vấn đề tương tự khi cả hai đều ở Cornell và anh ấy đã nghe Feynman thuyết trình, và sự hợp tác đó đã dẫn đến công thức Feynman-Kac.
Do đó, tính toán trực tiếp công thức Feynman-Kac, chúng tôi nhận được:
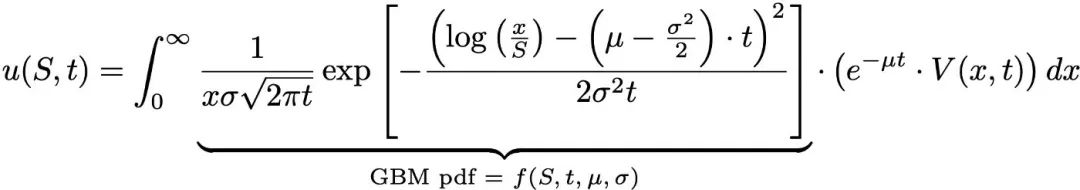
Đối với quyền chọn mua, giá trị trả về V(S,T) = max(SK,0), đối với quyền chọn bán, giá trị trả về V(S,T) = max(KS, 0), do đó, giá trị của quyền chọn mua và quyền chọn bán tại thời điểm t là:
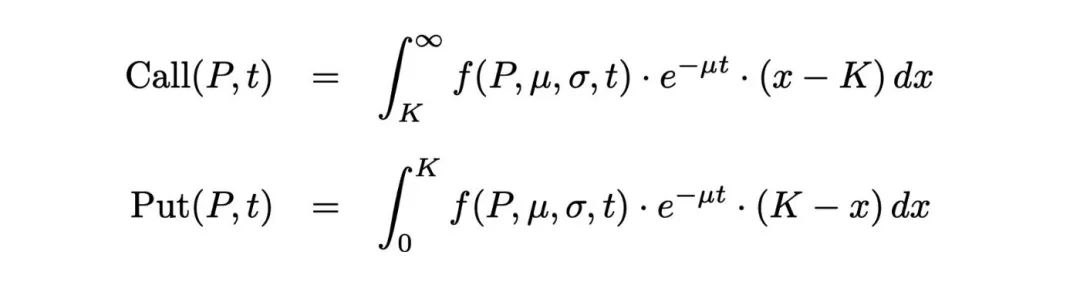
tiêu đề cấp đầu tiên
Giá tùy chọn Uniswap v3
Công thức Feynman-Kac giúp dễ dàng tính toán giá trị của các quyền chọn kỳ lạ. Chúng tôi sẽ áp dụng công thức Feynman-Kac để tính giá trị của các tùy chọn Uniswap v3.
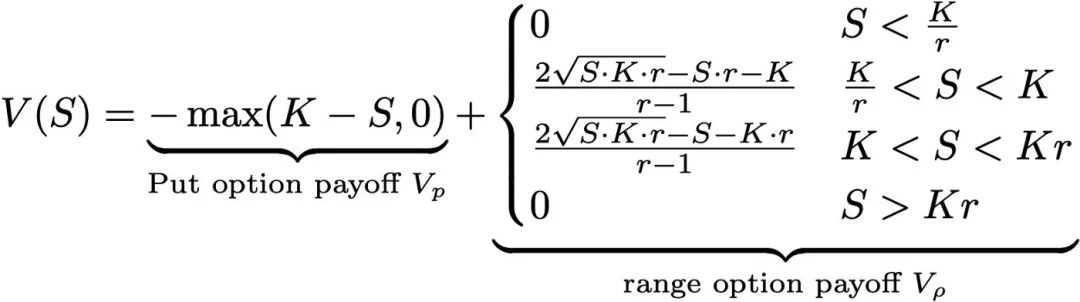
Để làm cho mọi thứ dễ dàng hơn một chút, trước tiên chúng tôi phân tách giá trị Uni v3 LP thành hai phần riêng biệt V(S, t) = V_p(S, t) + Vρ(S, t), trong đó V_p=-max( KS, 0) là mức hoàn trả của quyền chọn bán và mức hoàn trả theo phạm vi Vρ được cho bởi:
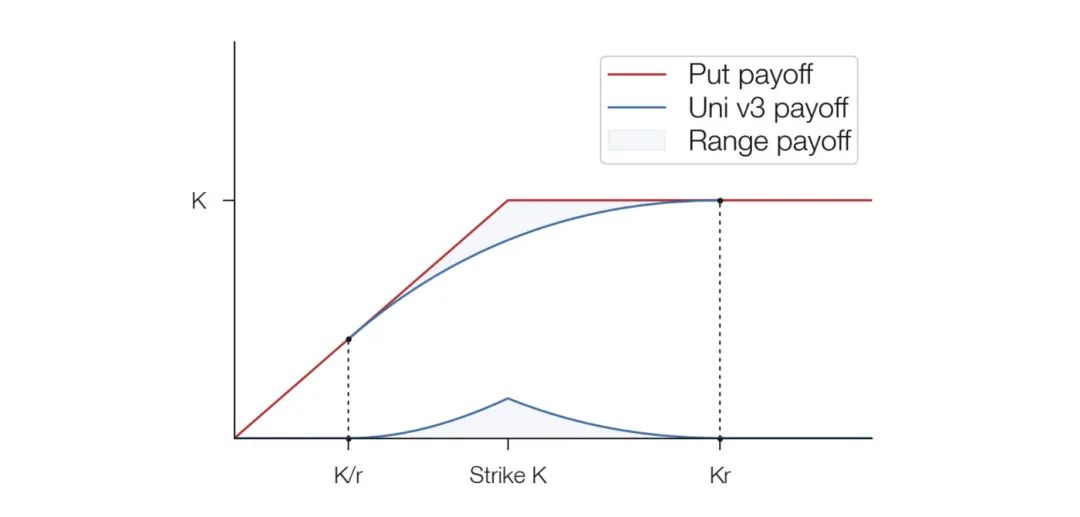
Chúng ta có thể thấy bằng đồ thị cách quyền chọn và lợi nhuận phạm vi liên quan đến giá trị của một vị trí Uni v3: lợi tức phạm vi là tối đa ở mức giá thực hiện và bằng 0 ở tỷ lệ trên/thấp (để đơn giản, tôi vẽ giá trị âm).
Sử dụng phép tách này, chúng ta có thể giải quyết một cách rõ ràng giá trị của tùy chọn Uni v3 tại thời điểm t bằng cách sử dụng công thức Feynman-Kac. Làm điều này, chúng tôi nhận được:

trong đó Put(S, t) là mức giá quen thuộc do Black-Scholes đưa ra cho quyền chọn bán ở bài tập K.
Thành phần "tùy chọn phạm vi" ρ(S,t) hoàn toàn dương, tương ứng với giá trị của phần phạm vi của vị trí LP. Bằng cách giải công thức Feynman-Kac, ta thu được một biểu thức khá phức tạp cho ρ(S,t):
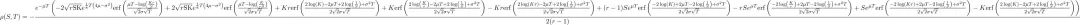
Mặc dù chúng ta không quan tâm đến các chi tiết của ρ(S,t) ngay bây giờ, nhưng chúng ta có thể thấy từ đồ thị rằng ρ(S,t) giống như sau:
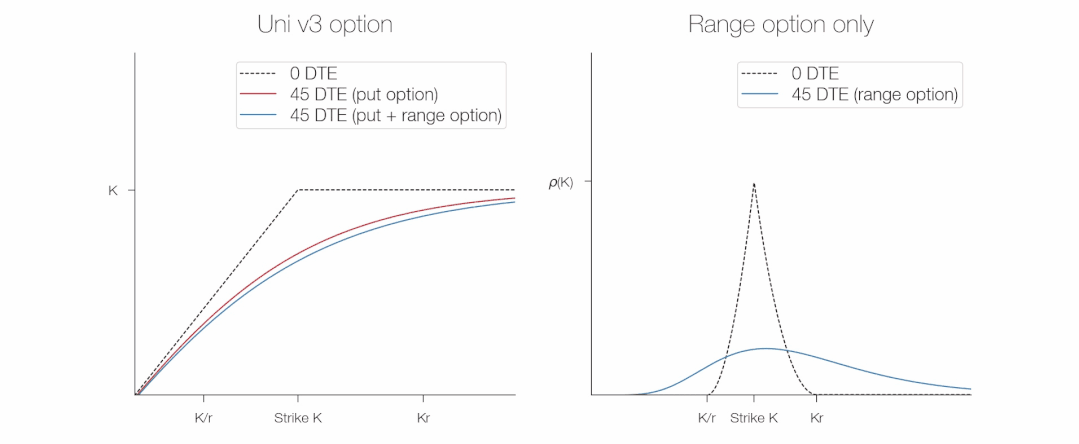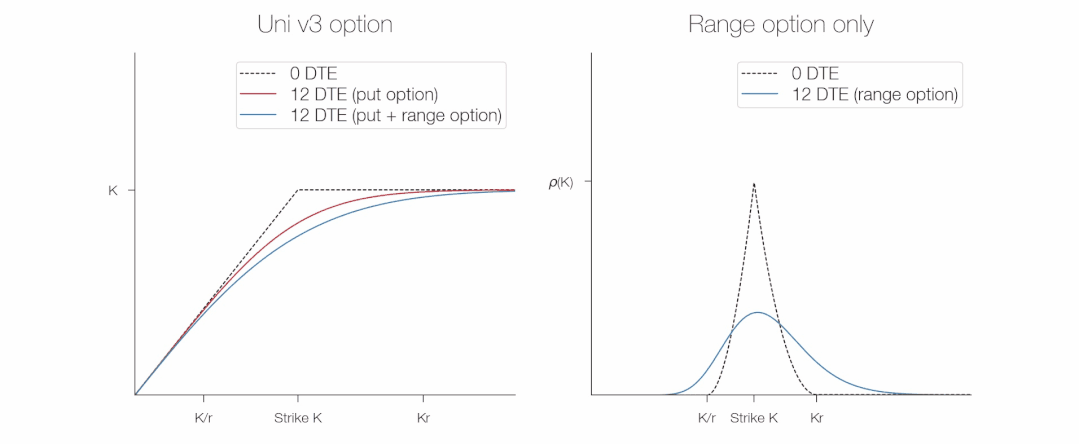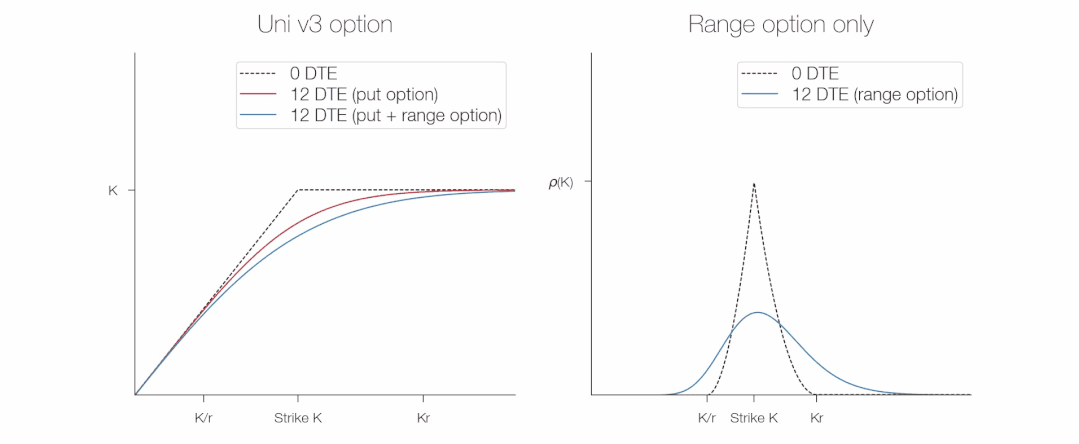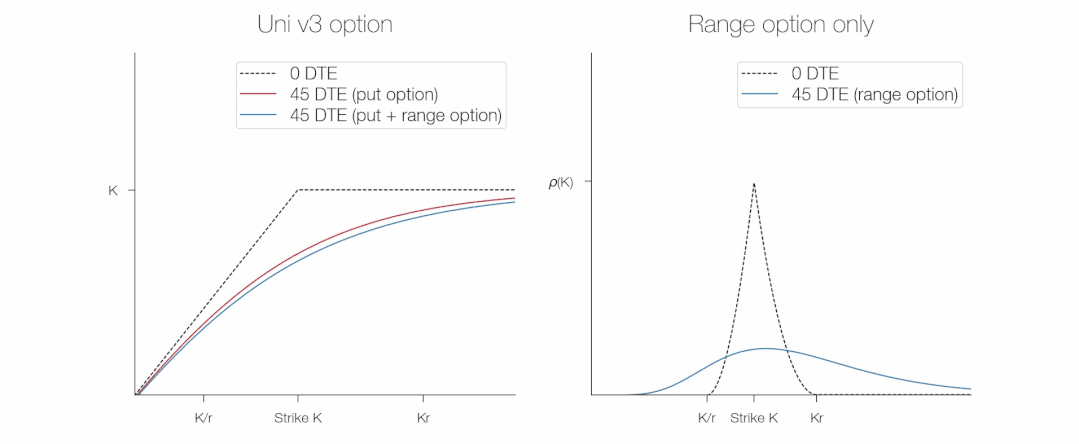
Chúng ta có thể làm cho biểu thức này đơn giản hơn không?
Biểu thức cho các giá trị vị trí Uni v3 khá phức tạp. May mắn thay, chúng ta có thể đơn giản hóa rất nhiều việc phân tích.
Như đã trình bày trong bài viết của tôi về cách tạo quyền chọn vĩnh viễn trong Uniswap v3, một giá trị gần đúng cho vị trí Uni v3 LP với hệ số phạm vi r là một quyền chọn bán thông thường tại thời điểm T_r, trong đó
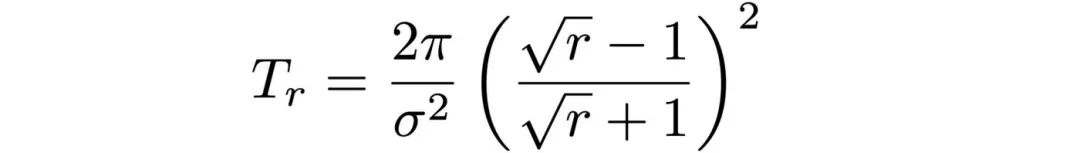
Do đó, chúng ta có thể rút gọn biểu thức định giá quyền chọn do công thức Feynman-Kac đưa ra thành một biểu thức đơn giản hơn khai thác mối quan hệ hệ số phạm vi/DTE ở trên. Cụ thể, chúng tôi nhận được:

Nói cách khác, giá trị của quyền chọn Uniswap v3 tương đương với quyền chọn bán hết hạn với một số ngày cố định trước khi hết hạn (DTE), vì vậy DTE > 0 khi hết hạn.
Trước khi hết hạn, giá của các tùy chọn Uni v3 sẽ vẫn bị ảnh hưởng bởi phân rã theta, nhưng gamma sẽ bị giới hạn ở gamma của các tùy chọn 45DTE.
Chúng ta có thể thấy trong hình bên dưới, so sánh phép tính gần đúng DTE cố định với phép tính tùy chọn Uni v3, rằng sự khác biệt giữa phép tính xấp xỉ quyền chọn bán DTE cố định và giải pháp chính xác là không đáng kể khi hệ số phạm vi nhỏ hơn 2 :
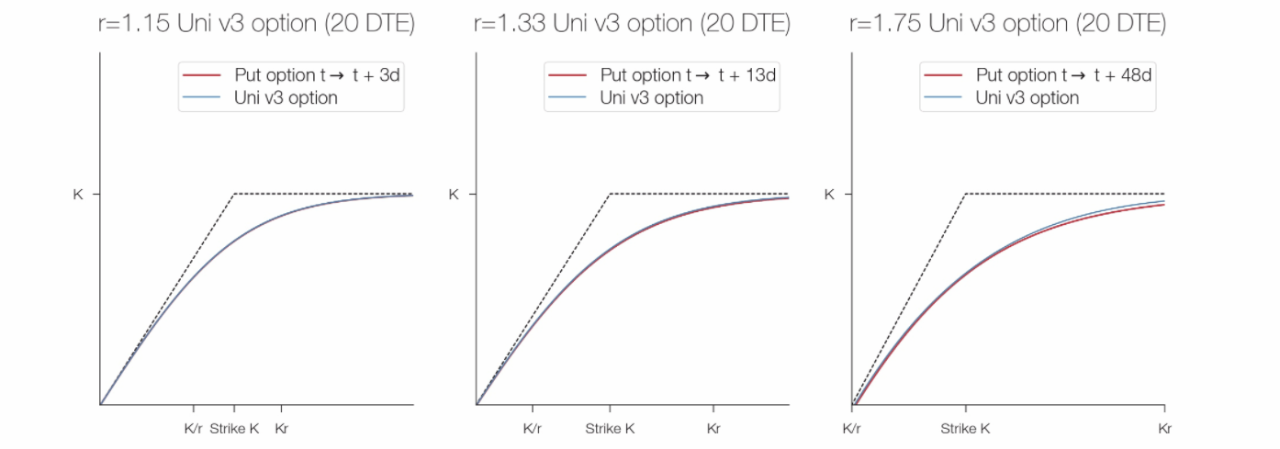
Hiện tại, lựa chọn duy nhất cho LP trên Uni v3 là giữ vị trí của họ cho đến khi họ tích lũy đủ phí để tạo ra lợi nhuận. Không có giao thức nào cho phép người dùng dễ dàng mượn/cho mượn các vị thế Uni v3 LP.
Tuy nhiên, nếu có một thỏa thuận như vậy, thì phí bảo hiểm mà các nhà cung cấp thanh khoản Uni v3 nhận được khi cho vay các vị trí LP của họ được đưa ra bởi mô hình Black-Scholes với một "DTE cố định" phụ thuộc vào hệ số phạm vi r. Ngược lại, nếu vị trí không được xem xét và phí chỉ được tính, thì phí cũng tích lũy.
Vì vậy, trong một thế giới nơi các vị trí Uni v3 LP được đúc/cho vay/mượn và giao dịch dưới dạng quyền chọn, một câu hỏi quan trọng là liệu có tốt hơn không nếu:
hoặc
hoặc
"Cho vay" quyền chọn trong khoảng thời gian T và tính phí bảo hiểm cố định
tiêu đề cấp đầu tiên
Duy trì vị trí LP
Đầu tiên, nếu tính thanh khoản được triển khai cho một báo giá duy nhất, lợi nhuận LP kỳ vọng của thanh khoản đơn vị ΔL là:

Trong đó γ là mức phí (ví dụ: 0,01, 0,003 hoặc 0,0005) và "Tick Liquidity" là lượng thanh khoản trong nhóm giá hiện tại. Hệ số của √(8/π)=1,5957691216… xuất phát từ việc tính toán thời gian dành cho giá với giả định rằng giá tuân theo chuyển động Brown hình học.
Mấu chốt ở đây là mức tăng thu nhập kỳ vọng là √T. Do đó, vì các khoản phí tích lũy tuyến tính theo thời gian cho các vị trí rộng hơn, nên chúng tôi sẽ chỉ xem xét các vị trí đơn lẻ.
Điều quan trọng, điều này có nghĩa là lợi nhuận LP sẽ phụ thuộc vào tổng kích thước của nhóm và tổng thanh khoản tại thời điểm được triển khai.
Trong ví dụ bên dưới, chúng tôi xem xét triển khai một vị trí ở mốc 3990 trong nhóm ETH-DAI-0,3%. Vì khối lượng giao dịch hàng ngày của nhóm này là 15,71 triệu USD, giá trị bị khóa của 3990 điểm là 70,60ETH = 281694 USD, lợi nhuận LP tương đối sẽ vào khoảng 1,6% mỗi ngày hoặc khoảng 30% mỗi năm (giả sử mức độ biến động hàng năm là 100%). ) .
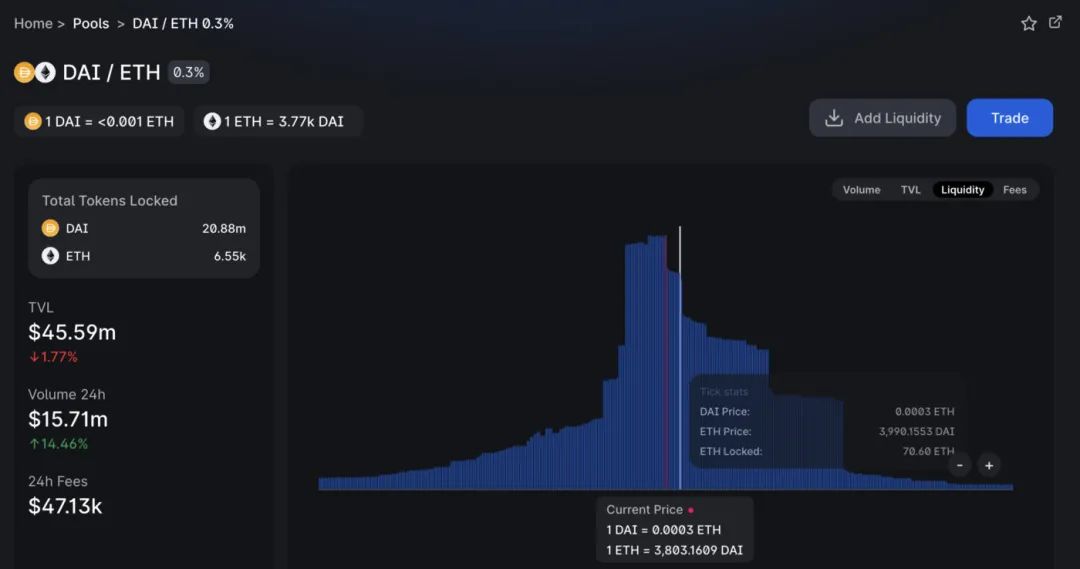
Ngược lại, triển khai cùng một tính thanh khoản vào nhóm tài sản như ETH-USDC-0,03% mang lại 1,37% mỗi ngày cho các vị trí LP, hoặc 26,2% mỗi năm. Một số nhóm tạo ra nhiều năng suất hơn những nhóm khác.
Một số pool có lợi nhuận kỳ vọng rất cao, chủ yếu là do tính thanh khoản trên mỗi pip tương đối thấp so với khối lượng giao dịch của chúng.
Ví dụ: một mã thông báo mới được liệt kê như RBN chỉ có 500.000 đô la giá trị bị khóa với giá trị hiện tại là 25 triệu đô la.
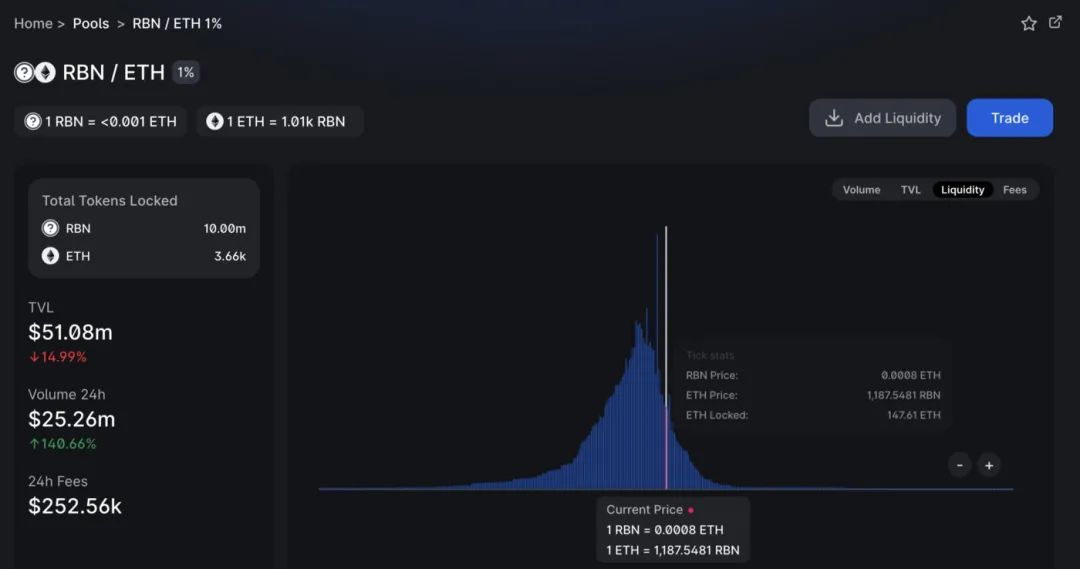
Mặt khác, một người dùng có thể muốn tạo một vị thế Uni v3 LP và cho một người dùng khác mượn nó trong một khoảng thời gian T với phí bảo hiểm.
Cụ thể, phí bảo hiểm nhận được sẽ là:
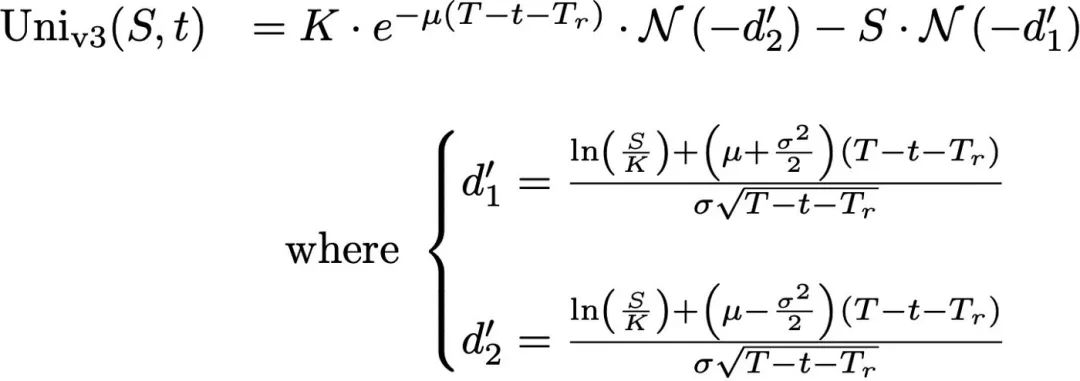
Đây là biểu thức quen thuộc cho giá trị của quyền chọn bán khống, ngoại trừ việc thời gian chuyển đổi theo t→(t+T_r).
Biểu thức này sẽ phụ thuộc vào cơ sở cụ thể, giá thực hiện K, độ biến động ngụ ý σ và thời gian hết hạn t. Nếu chúng ta coi quyền chọn được đúc "bằng tiền", với K bằng với giá hiện tại tại giá thực hiện của vị thế LP, sau đó là quyền chọn bán Giá trị là:
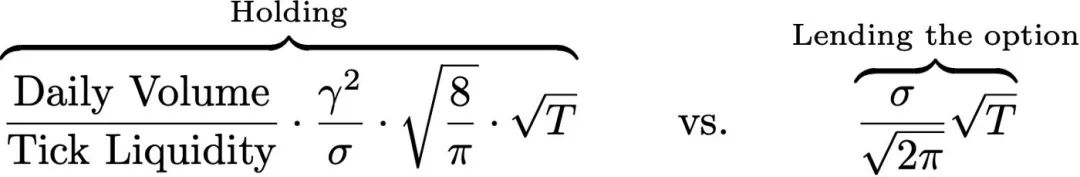
Thật thú vị, biểu thức này cũng phụ thuộc vào căn bậc hai của thời gian. Điều này có nghĩa là chúng tôi có thể so sánh trực tiếp phí bảo hiểm mà chúng tôi nhận được trên mỗi đơn vị thanh khoản được triển khai với lợi nhuận kỳ vọng mà chúng tôi sẽ nhận được bằng cách giữ các vị trí LP và thu phí.
Nếu chúng ta xem xét vị thế một lần đánh dấu, thì T_r sẽ bằng 0 và (Tt) sẽ là thời gian nắm giữ của vị thế (nếu được giữ cho đến khi hết hạn).
Do đó, chúng ta chỉ cần so sánh các yếu tố nhân với số hạng √T để tìm ra chiến lược nào có lợi nhất:
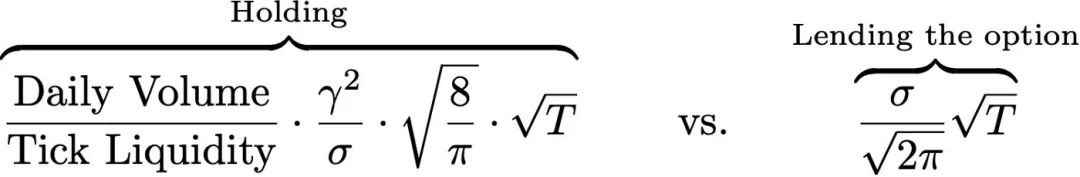
Giả sử mức biến động hàng năm là 100%, điều này có nghĩa là quyền chọn nắm giữ sẽ chỉ mang lại lợi nhuận cao hơn quyền chọn cho vay nếu tỷ lệ khối lượng hàng ngày/thanh khoản tức thời lớn hơn:
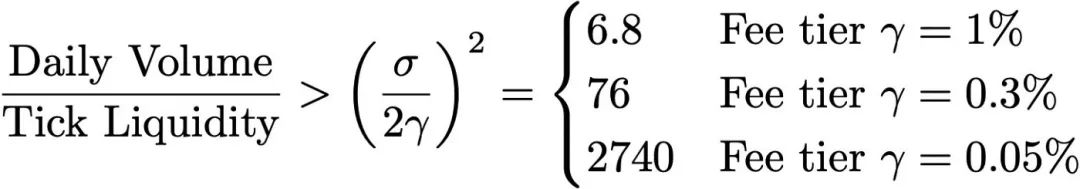
Khối lượng thực tế hàng ngày, thanh khoản đánh dấu và độ biến động đã thực hiện có thể cần được tính toán cho từng nhóm để xác định chính xác liệu các tiêu chí trên có được đáp ứng hay không (có thể thay đổi đối với từng nhóm).
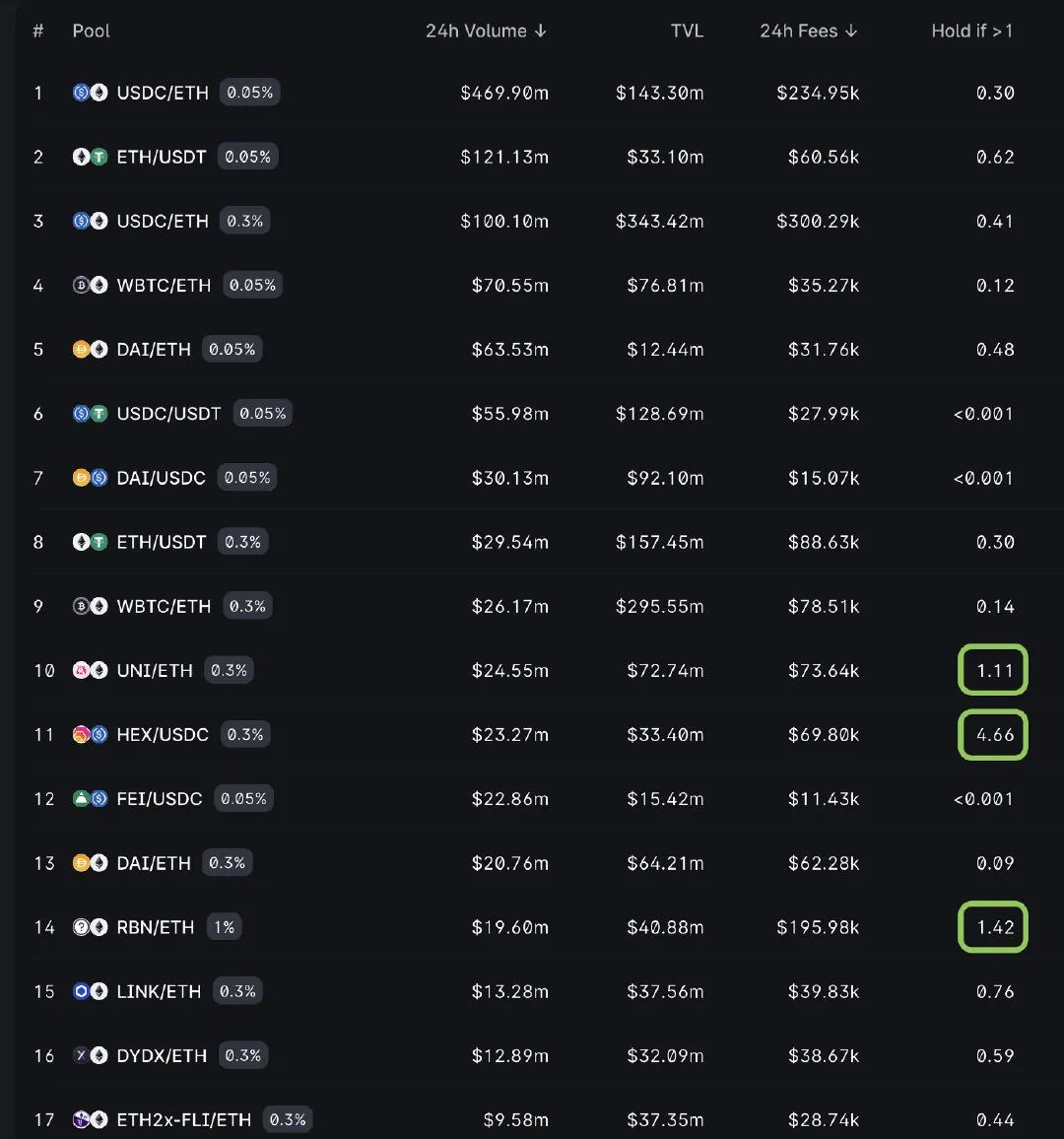
Một số nhóm có khối lượng giao dịch hàng ngày thực sự cao so với tính thanh khoản mà chúng khóa. Chỉ khi tỷ lệ nắm giữ lớn hơn 1, việc nắm giữ các vị trí của các nhóm tài sản này sẽ tạo ra lợi nhuận kỳ vọng cao hơn phí quyền chọn.
Hiện tại, chỉ các nhóm UNI/ETH, HEX/USDC và RBN/ETH được đánh dấu ở trên mới có thể tạo ROI cao hơn. tỷ lệ nắm giữBất kỳ cặp tiền tệ nào < 1 sẽ hoạt động kém hiệu quả, hãy cho vay chúng dưới dạng tùy chọn.
tiêu đề cấp đầu tiên
điểm chính
Kết quả của chúng tôi cho thấy rằng vị thế Uni V3 tương tự như việc bán khống quyền chọn bán, trong hầu hết các trường hợp, người mua quyền chọn sẽ cho người mua quyền chọn vay và thu phí bảo hiểm, thay vì chỉ đơn giản là nắm giữ quyền chọn bán và thu phí.
Điều này có nghĩa là gì Đầu tiên, nó gợi ý rằng việc xây dựng một thị trường quyền chọn lành mạnh dựa trên Uniswap v3 (hoặc pool thanh khoản tập trung sắp ra mắt của SushiSwap) có thể tăng lợi nhuận mà các nhà cung cấp thanh khoản thu được.
Thứ hai, LP không chỉ có thể tạo thêm thu nhập, người mua quyền chọn còn có thể bảo vệ khoản đầu tư của họ bằng cách mua quyền chọn bán. Tùy chọn cặp ETH-stablecoin có thể được xử lý hiệu quả bằng các giao thức như Opyn, Pods Finance hoặc Lyra Finance, nhưng sẽ rất khó để xây dựng hợp đồng giao dịch thông minh cho các tùy chọn trên mọi cặp tài sản có thể (có hàng nghìn thị trường tồn tại tài sản mã hóa đuôi dài Uniswap ).
Cuối cùng, cần phải có một sự thay đổi về văn hóa khi mọi người giải thích cách các vị trí thanh khoản tập trung được triển khai trên Uniswap v3 hoặc SushiSwap. Mặc dù các AMM sản phẩm cố định dễ hiểu và dễ quản lý hơn nhưng chúng dễ bị tổn thất tạm thời đáng kể và sử dụng vốn rất kém hiệu quả so với các AMM thanh khoản tập trung.
Bài viết này đến từ cộng đồng tài chính phi tập trung và được sao chép với sự cho phép.
Bài viết này đến từ cộng đồng tài chính phi tập trung và được sao chép với sự cho phép.



