Authors: Jonathan W., Vincent H., and Yi Sun

author

author

Introduction

Introduction

Pairing-based cryptography2 (PBC) builds on elliptic curve cryptography4 where a mathematical object called elliptic curve pairing3 exists. Although pairs are relatively complex to define, they are the basis for many cryptographic objects in modern developments in zero-knowledge cryptography: BLS digital signatures, KZG polynomial commitments, and zkSNARKs.

Due to this key role in the ZK ecosystem, implementing pairings in zkSNARKs greatly expands the range of addressable cryptographic constructions and increases the reflectivity of SNARKs. In particular, we envision ZK Identity for applications (ZK Identity5), blockchain scaling, and programmable SNARKs. The final "unlock" could lead to a future where anyone can freely combine and combine different SNARKs on the fly.

Since pairing involves many complex elliptic curve operations, implementing them in zkSNARKs presents many challenges. First, for elliptic curve algorithms on unnatural domains, we have to use zk-ECDSA6's large integer and ECC optimizations, but accommodate the fact that pairing our curves with BLS12-381 involves operating on domain extensions. Second, Miller's computational pairing algorithm7 allows many optimizations in standard computational models, which we port over to the zkSNARK setting. Finally, even the final optimized circuit can be quite large due to the complexity of pairing calculations, which means that some infrastructure best practices are required to accommodate the Circom tool stack.

In this series of articles, we present a proof-of-concept Circom implementation of optimal Ate pairing on the BLS12-381 curve, and an example application in BLS signature verification. We then outline other potential applications, such as recursive SNARKs and multinomial commitment verification, which we believe can be easily generalized.

cycle pairing

We implemented the circular pairing circom-pairing8 codebase, which provides unaudited ZK circuits for the following operations on the BLS12-3819 curve:

• Tate pairings are one of the simplest elliptic curve pairings. The algorithm satisfies the bilinear characteristic, is suitable for the field of cryptography, and plays a very good role in checking the calculation of elliptic curves and the correct realization of the algorithm.

• Best pairing: The best pairing is the one most used in practice. The computation is similar to Tate pairing (using Miller's algorithm, which we will discuss in a future post); however, fewer steps are involved, and the algorithm at each step is more complex, with the end result being a shorter total computation.

• BLS10 signature verification (short public key): signature verification allows checking a BLS signature. Given a signature s, generator G, public key xG, and hash hash, the verification circuit converts hash to elliptic curve point H(m), using maptoG2 The circuit below then verifies that s is indeed a signature generated by the given public key and message. BLS signature verification involves evaluating two optimal Ate pairings to verify this e(s,G) = e(H(m), xG) , where e represents the best Ate pairing

• Hash to Curve: maptoG2's BLS signature verification operation works by computing point pairs on an elliptic curve. The message being signed must first be hashed into a value. This hash value is then converted into a point on the elliptic curve; the hash-to-curve circuit performs this conversion.

More detailed documentation of our circuit is available here. These circuits have not been reviewed and are not intended to be used as libraries for production-grade applications.

demo

To illustrate our circuit, we implemented a demo at zkpairing.xyz11 that allows users to generate proofs of the validity of any BLS signature (in a specific input format). If users don't have a specific BLS signature they can specify any block number on the Ethereum beacon chain, and the demo will parse the block data into the appropriate format and generate a proof block that verifies that validator's signature. For each proof, we provide all the data - in three small files - that anyone can use to verify the proof on their own computer!

benchmark

All benchmarks are run on 32 cores 3.1 GHz, 256G RAM, 1T hard drive and 400G switch (AWS r5.8 xlarge instance).

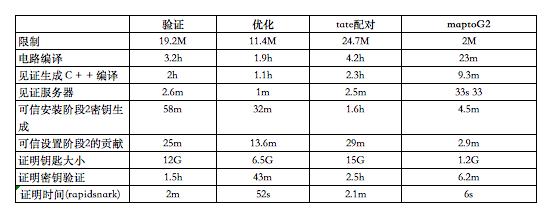
run large circuits

Note that verification and Tate pairing are very large circuits, so they require special hardware and setup to run. In particular, the witness must be generated using C++, attestation using rapidsnark, and keys generated using a patched version of Node.js without garbage collection. All of this had to be done on a machine with a lot of memory; our setup workflow is detailed in the Best Practices for Large Circuits12 document.

What can we do with zkPairing?

Because pairing is a core component of many cryptographic protocols, zkSNARKs for pairing computations allow us to put the following high-level primitives into SNARKs:

• BLS signature verification: Boneh-Lynn-Shacham (BLS) digital signature is a signature scheme based on elliptic curve pairing. Due to the ability to efficiently compute aggregate and threshold signatures using BLS, it is currently used in blockchains such as Ethereum 2.0, ZCash, and Dfinity. Verification of BLS signatures involves a pairing check to see if two elliptic curve pairs are equal, and is therefore directly enabled via zkPairing. This unlocks potentially scalable applications such as lightweight clients and bridged signature aggregation.

• Recursive SNARK verification: Because Groth16 proof verification only involves pair checking, SNARK-ing pairing allows SNARK-ing the entire verification algorithm, called recursive verification. This allows us to build a zkSNARK of zkSNARKs...infinite advertisements, enabling developers to build proofs of different SNARKs, rather than building a single large SNARK and greatly increasing the complexity of possible SNARKs. We are adapting our circuit to recursively Groth16 validate the BN254 and hope to publish a proof of concept in the near future.

• KZG Polynomial Commitment Verification: KZG Polynomial Commitment is the basis of PlonK, one of a new generation of zkSNARKs with a general trusted setup. Because verifying a KZG commitment involves a pair check, zkSNARK-ing pairings allows us to verify anything built on top of a KZG commitment in a SNARK, including PlonK verification itself!

thank you

thank you

The project was built during the ZK Identity Working Group at 0xPARC with support from the ZKxZK Gitcoin Foundation.

We have borrowed and shared many technologies related to circom-ecdsa, especially in the optimization of large integer and elliptic curve algorithms. For example, we use xJsnark's large integer multiplication optimization.

refer to

refer to

• https://github.com/yi-sun/circom-pairing

• https://en.wikipedia.org/wiki/Pairing-based_cryptography

• https://medium.com/@VitalikButerin/exploring-elliptic-curve-pairings-c73c1864e627

• https://en.wikipedia.org/wiki/Elliptic-curve_cryptography

• https://0xparc.org/blog/zk-id-2

• https://0xparc.org/blog/zk-ecdsa-2

• https://crypto.stanford.edu/pbc/notes/ep/miller.html

• https://github.com/yi-sun/circom-pairing

• https://hackmd.io/@benjaminion/bls12-381

• https://datatracker.ietf.org/doc/html/draft-irtf-cfrg-bls-signature-04

• https://zkpairing.xyz/

• https://hackmd.io/V-7Aal05Tiy-ozmzTGBYPA?view